算法学习专栏——栈（一）

前言

先照顾一下基础薄弱的同学，介绍一下什么是栈。

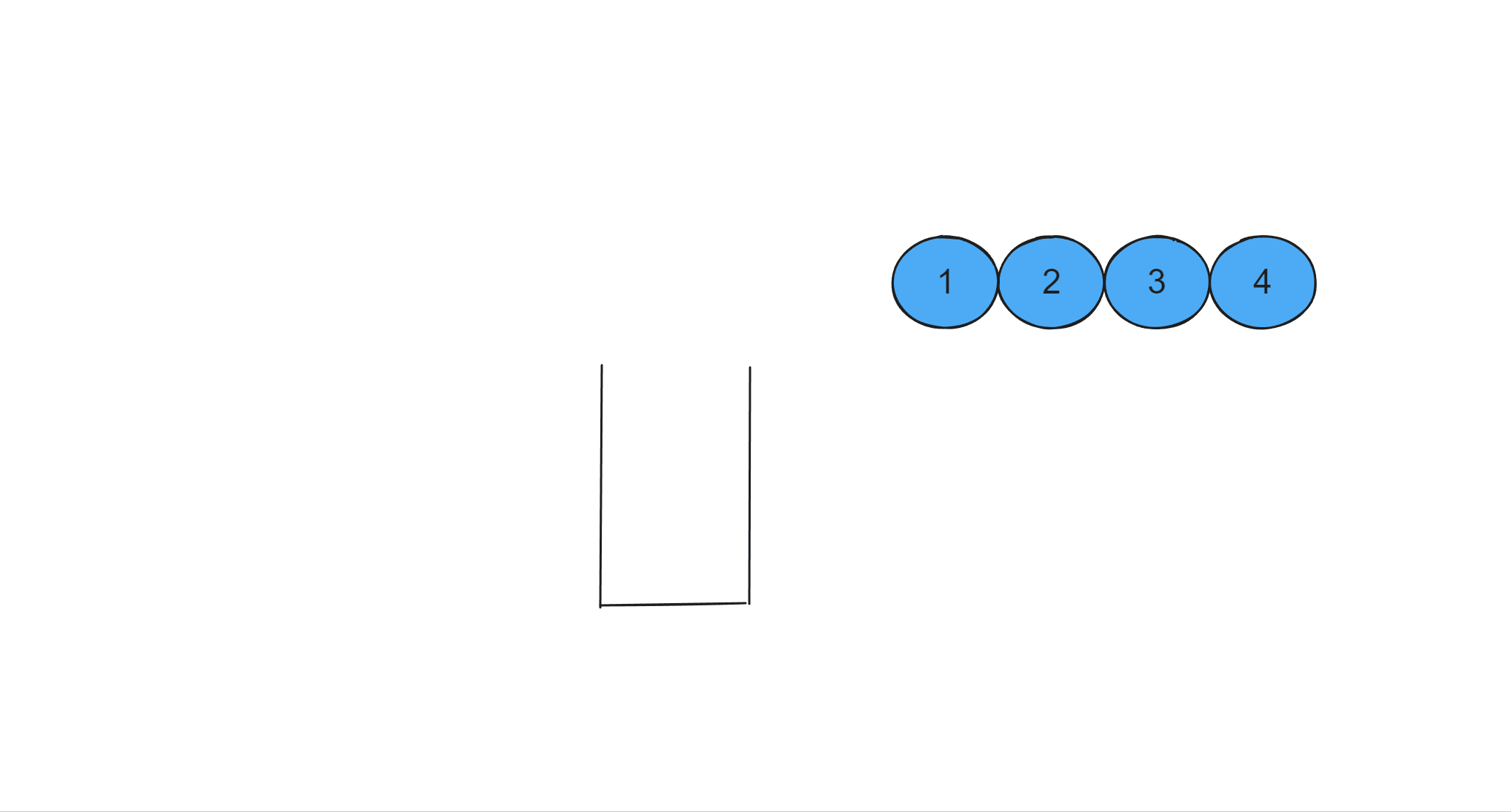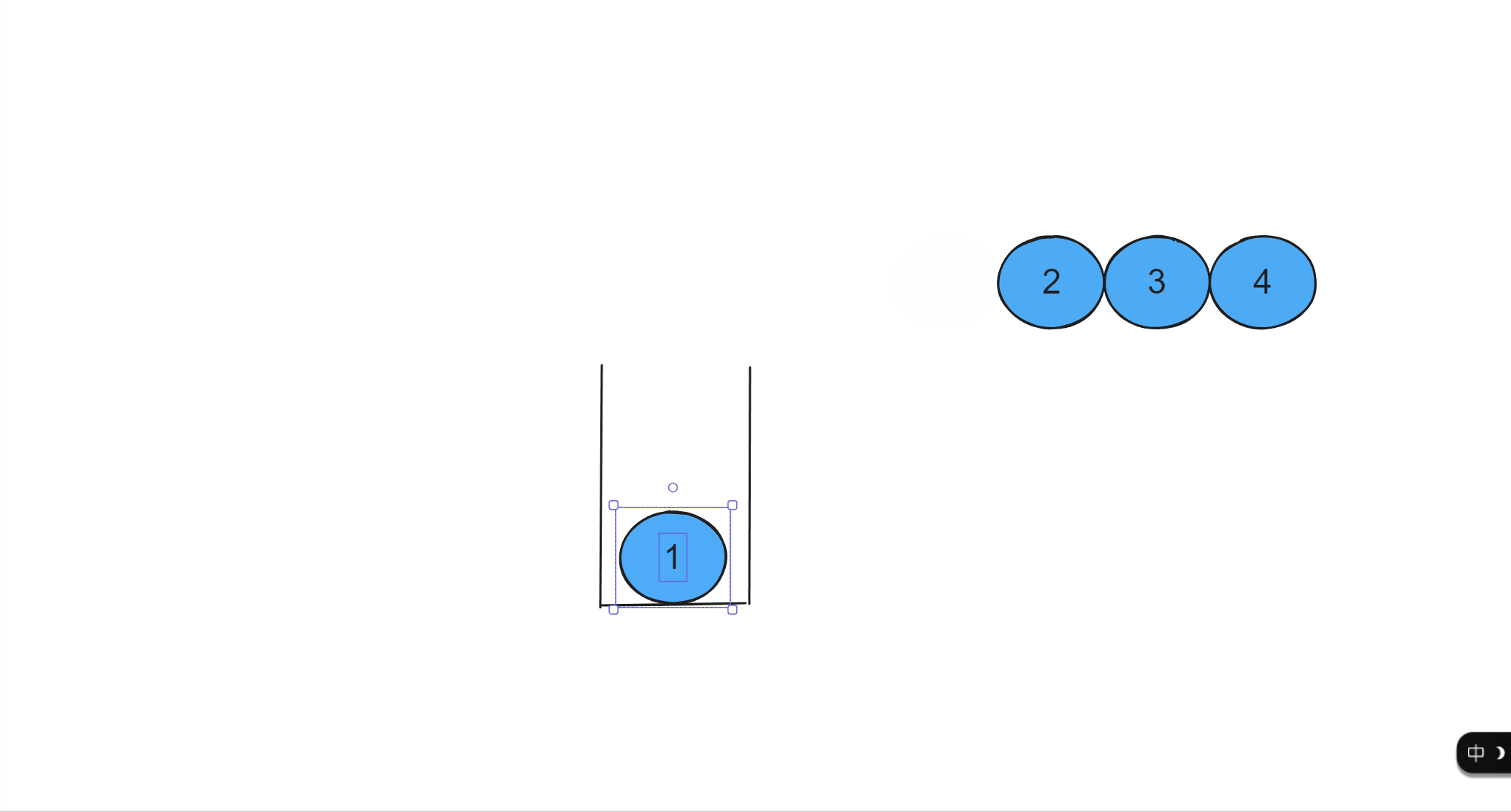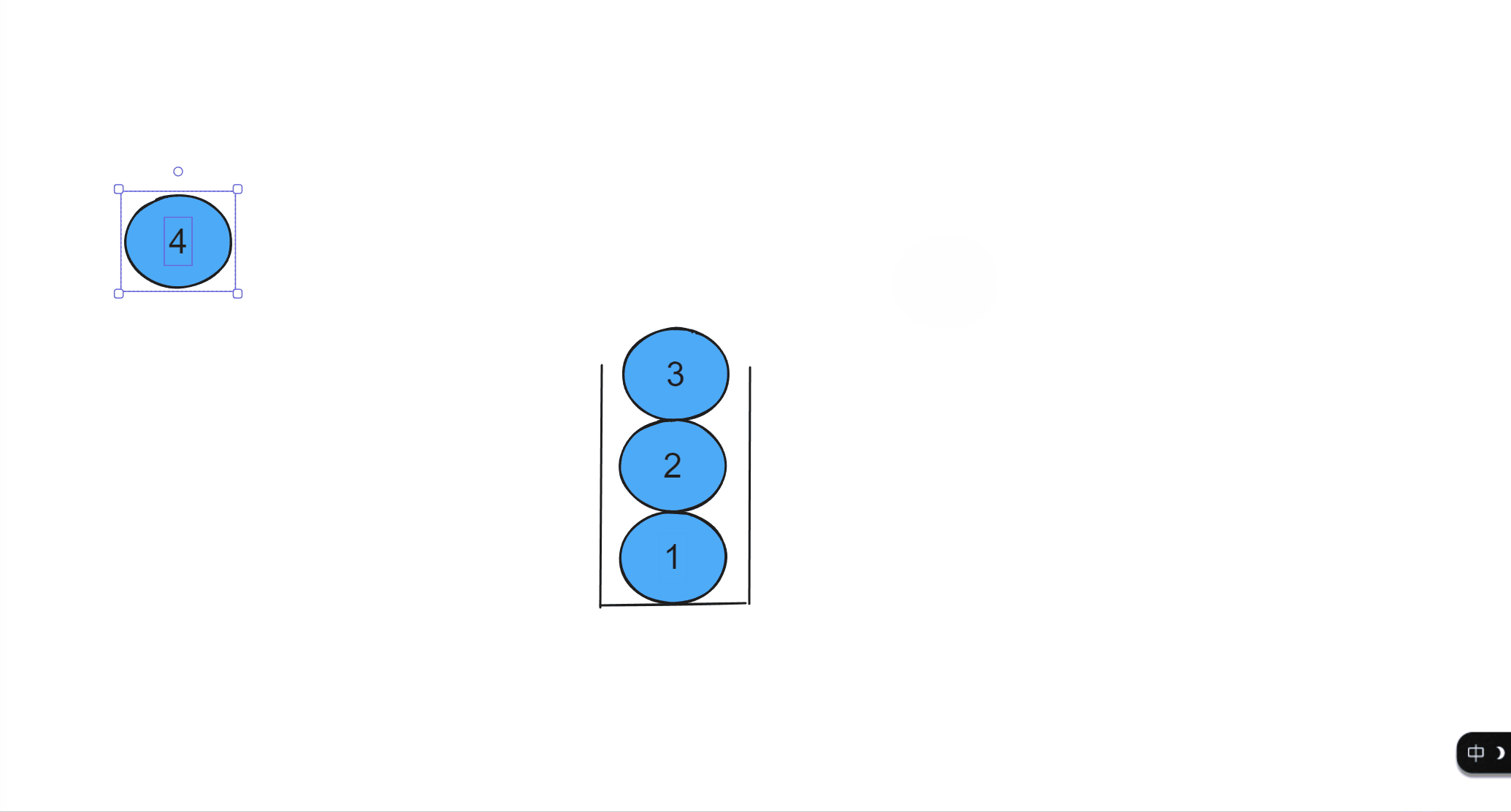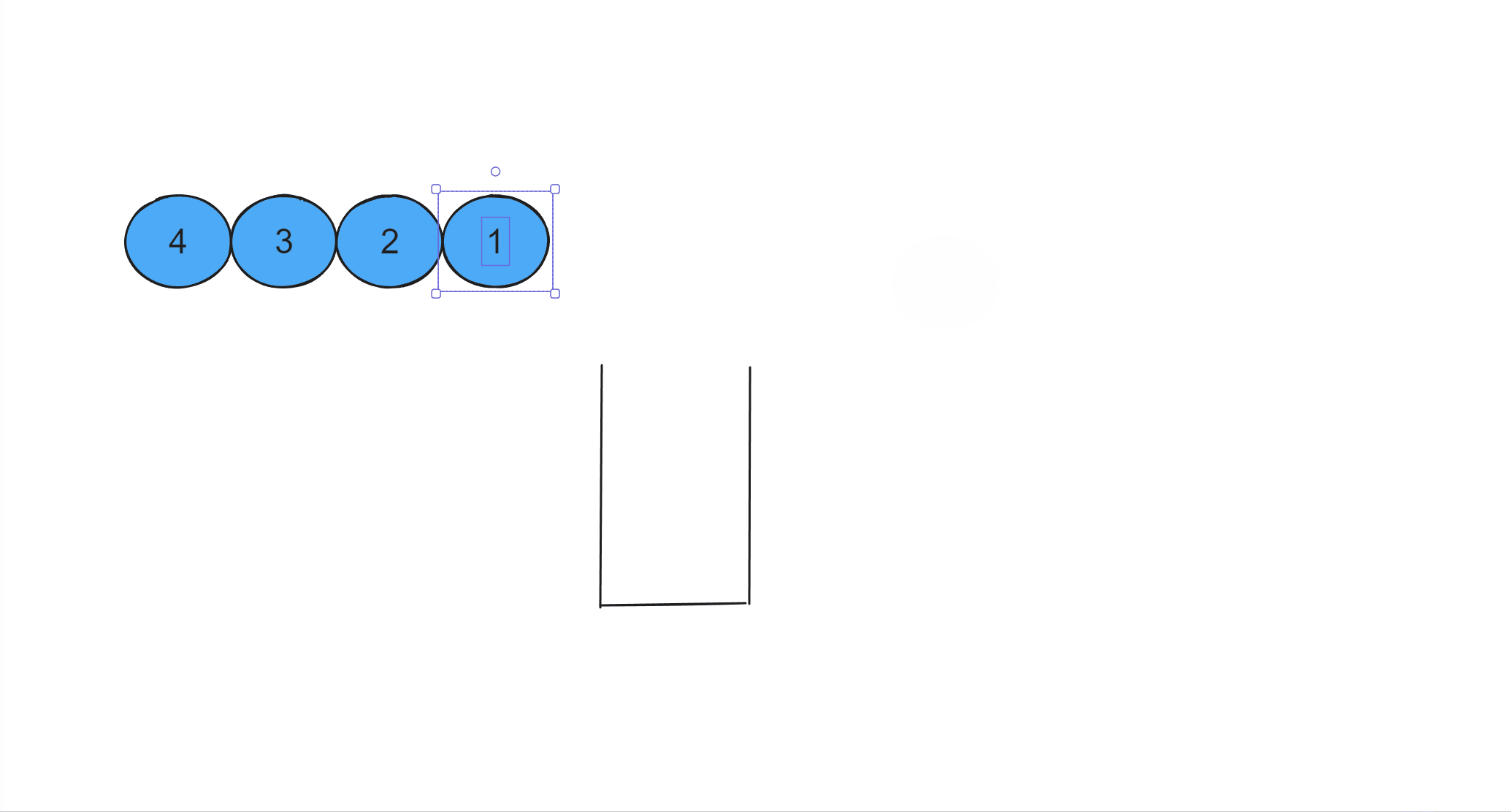
栈就是一个头开底闭的一个盒子，首先看一下下面的动画视频来了解一下栈

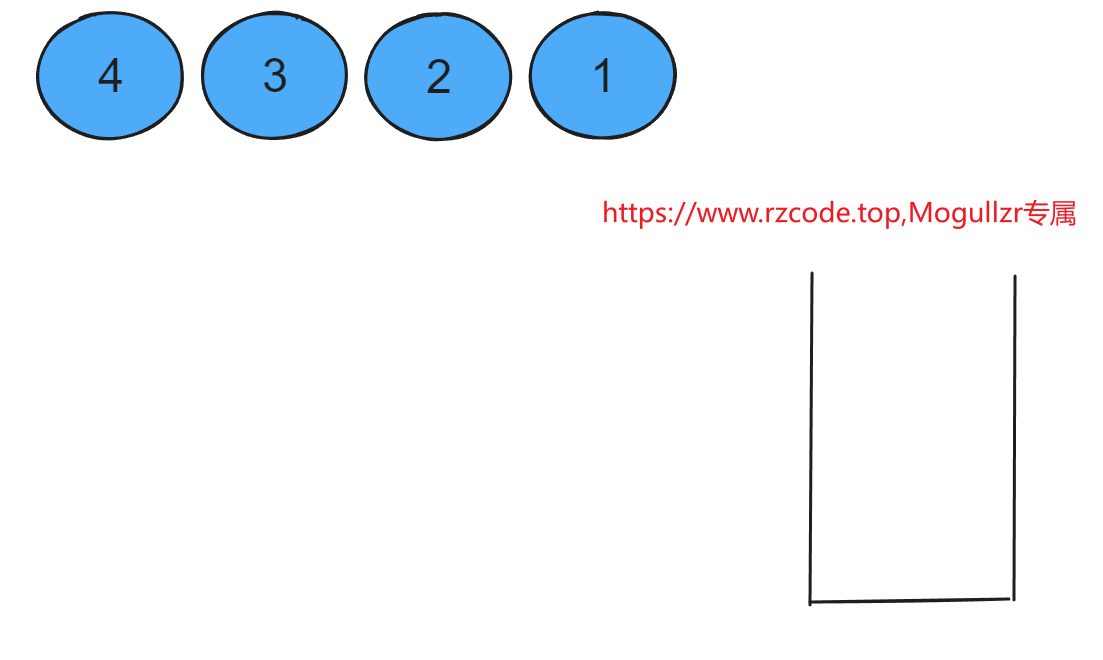
进栈操作（栈顶插入一个元素）：这个过程是一个一个进的，球1进完，球2再进

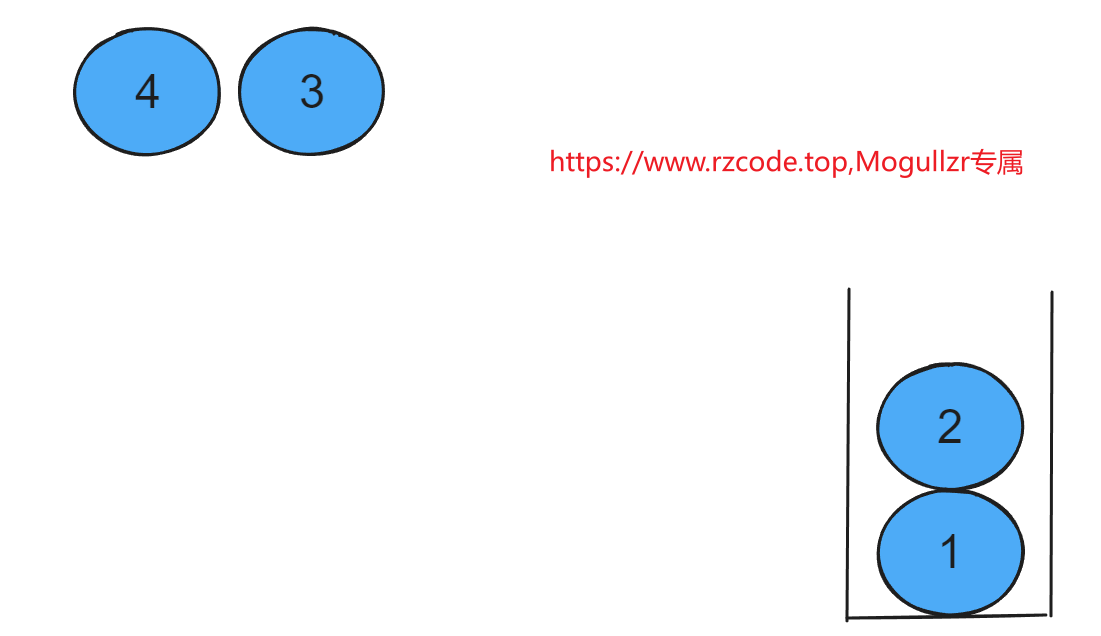
出栈操作（从栈顶弹出一个数）：必须按照从上往下的顺序弹出栈里元素操作，比如下图，不可以先将球1拿出来，必须先将球2拿出来之后再拿球1

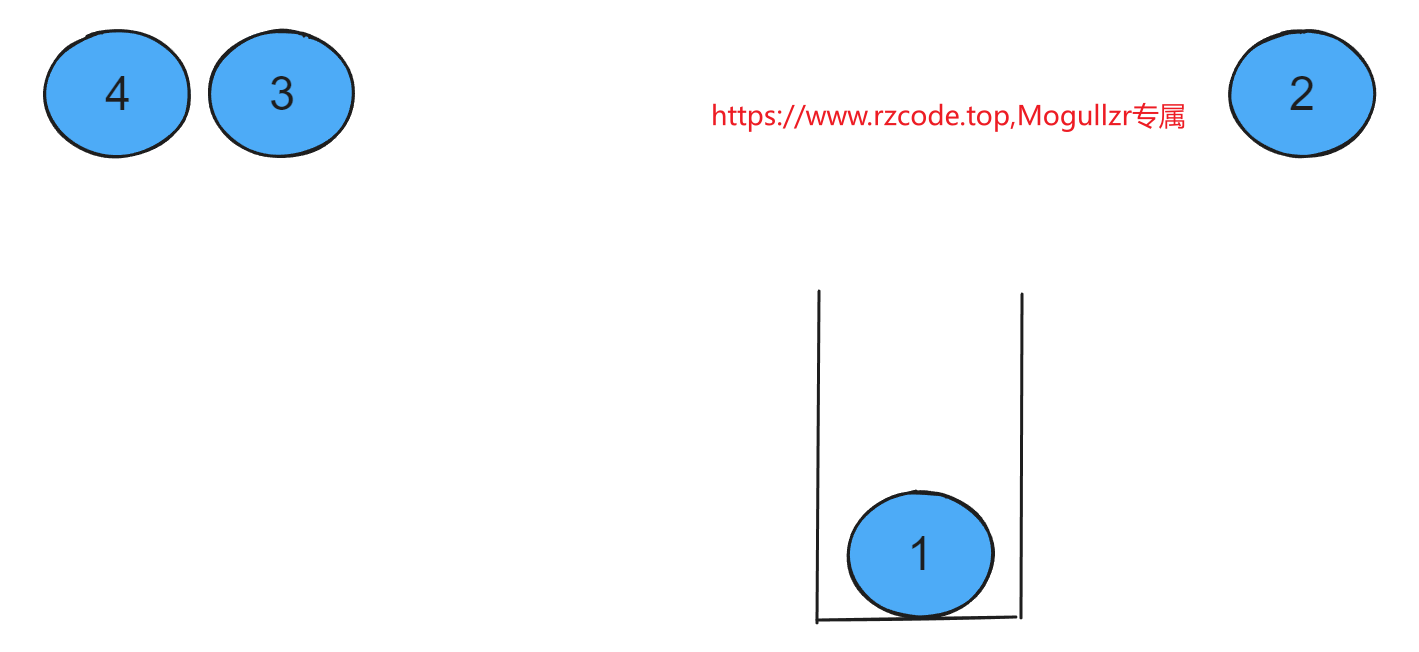
空栈：栈内没有小球（元素）

一、模拟栈（简单-）

实现一个栈，栈初始为空，支持四种操作：

push x – 向栈顶插入一个数 x；
pop – 从栈顶弹出一个数；
empty – 判断栈是否为空；
query – 查询栈顶元素。

现在要对栈进行 M 个操作，其中的每个操作 33 和操作 44 都要输出相应的结果。

输入格式

第一行包含整数 M，表示操作次数。

接下来 M 行，每行包含一个操作命令，操作命令为 push x，pop，empty，query 中的一种。

输出格式

对于每个 empty 和 query 操作都要输出一个查询结果，每个结果占一行。

其中，empty 操作的查询结果为 YES 或 NO，query 操作的查询结果为一个整数，表示栈顶元素的值。

数据范围

$$
1≤M≤100000\
1≤x≤109
$$

所有操作保证合法。

输入样例：

10
push 5
query
push 6
pop
query
pop
empty
push 4
query
empty

输出样例：

5
5
YES
4
NO

思路

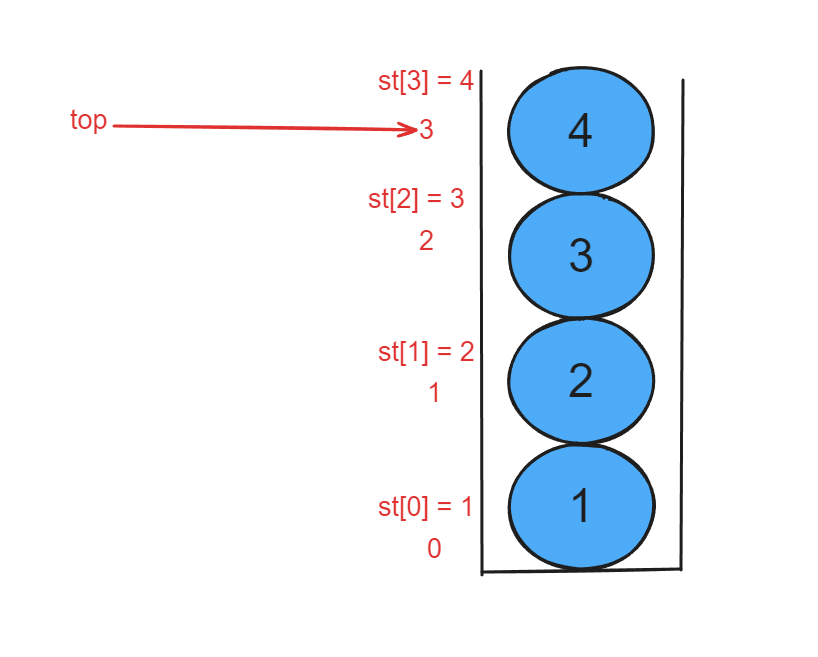
此时的top=3，指向的是元素st[3] = 4。

代码

答案（请自己先思考一下再参考）

        
#include < iostream>
using namespace std;
const int N = 1e5 + 10;
int st[N],top;
int n;
// 初始化栈
void Init()
{
    top = -1; // top是栈顶，一开始没有元素，初始化为-1,top指向的就是栈顶部元素的下标，请看上图理解top
}
int main()
{
    ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
    cin >> n;
    Init();//1、初始化栈
    while (n--)
    {
        string s;
        cin >> s;
        if (s == "push") // 入栈
        {
            int x;
            cin >> x;
            st[++top] = x;
        }
        else if (s == "pop") // 出栈
        {
            top--;
        }
        else if (s == "empty") // 判断栈是否为空
        {
            if(top == -1) cout << "YES\n"; 
            else cout << "NO\n";
        }
        else // 查询栈的顶部元素
        {
            cout << st[top] << '\n';            
        }
    }
}

二、火车进栈（这道题目大家可以先放着，因为涉及到了后面的一个递归算法，所以不会写也没有很大的关系，简单）

这里有 n 列火车将要进站再出站，但是，每列火车只有 11 节，那就是车头。

这 n 列火车按 1 到 n 的顺序从东方左转进站，这个车站是南北方向的，它虽然无限长，只可惜是一个死胡同，而且站台只有一条股道，火车只能倒着从西方出去，而且每列火车必须进站，先进后出。

也就是说这个火车站其实就相当于一个栈，每次可以让右侧头火车进栈，或者让栈顶火车出站。

下面是火车进站的一种方式的动态图：

现在请你按字典序输出前 20 种可能的出栈方案。

输入格式

输入一个整数 n，代表火车数量。

输出格式

按照《字典序》输出前 20 种答案，每行一种，不要空格。

数据范围

1≤n≤20

输入样例：

输出样例：

思路

使用最基础的dfs的思想

代码

答案（请自己先思考一下再参考）

        
#include< iostream>
#include< vector>
using namespace std;
const int N = 2e1 + 5;
int n, remain = 0;
int tt, stk[N];
vector< int> path;
void dfs(int u) {
    if (u == n + 1) { // edge：边界
        if (++remain > 20) {
            exit(0);
        }
        for (auto x:path) { //输出路径中的
            cout << x;
        }
        // 如果没有数字可用了, 那么输出一下path+栈中的数字
        for (int i = tt - 1; i >= 0; i--) { //输出栈中剩下的(后进先出
            cout << stk[i];
        }
        cout << endl;
        return;
    }
    if (tt) {
        path.push_back(stk[--tt]);
        dfs(u);
        stk[tt++] = path.back();
        path.pop_back();
    }
    stk[tt++] = u;
    dfs(u + 1);
    tt--;
}
int main() {
    cin >> n;
    dfs(1);
    return 0;
}

三、有效括号（简单+）

小刘在大一下学期学习到了数据结构栈操作中的经典例题，但是他不会写，请帮助他编写C++代码解决下列例题。

给定一个只包括 ‘(’，‘)’，‘{’，‘}’，‘[’，‘]’ 的字符串 s ，判断字符串是否有效。

有效字符串需满足：

左括号必须用相同类型的右括号闭合。

左括号必须以正确的顺序闭合。

每个右括号都有一个对应的相同类型的左括号。

示例 1：

1 2	`输入：s = “()” 输出：true`

示例 2：

1 2	`输入：s = “()[]{}” 输出：true`

示例 3：

1 2	`输入：s = “(]” 输出：false`

提示：

1	`1 <= s.length <= 104`

注意：s 仅由括号 ‘()[]{}’ 组成

思路

代码中有解释，基本就是按照栈的基本操作思路实现的。

代码

答案（请自己先思考一下再参考）

        
#include < iostream>
#include < algorithm>
#include < stack>
using namespace std;
int main()
{
    string s;
    cin >> s;
    if(s.size()== 0)
    {
        cout << "false"; 
        return 0;
    }
    if(s.size()%2 == 1)
    {
        cout << "false";
        return 0;
    }
    if(s[0] &&(s[0]== ']' || s[0]== '}'||s[0] == ')'  )) {
        cout <<  "false";
        return 0;
    }
    int length = s.size() ; 
    stack< char> charst ; 
    char current_deal_char; // 当前处理的字符
    for(int i = 0 ;i < length ; i++) {
        if(charst.size() == 0 && (s[i]== ']' || s[i]== '}'||s[i] == ')'  )){
            cout << "false";
            return 0;
        }
        // 如果遇到左括号，入栈
        if(s[i] == '(' || s[i] == '{' || s[i] == '['){ 
            charst.push(s[i]) ; 
        } 
        else if(s[i]== ']' || s[i]== '}'||s[i] == ')'){
            // 如果遇到右括号
            char tmp = charst.top() ; 
            //cout<< tmp << endl; 
            if(s[i] ==']' && tmp =='[') {
                // 如果相等，则抵消
                charst.pop() ; 
            }else if(s[i] == ')' && tmp == '(') {
                charst.pop() ; 
            }else if(s[i] == '}' && tmp == '{') {     
                charst.pop() ; 
            }else {
                cout << "false";
                return 0;
            }
        }
    }
    // cout<< charst.size()<< endl;
    cout << (charst.empty() == 1 ? "true" : "false");
}

算法学习专栏——栈（二）上一篇

算法学习专栏——进制转换类型题目下一篇