算法学习专栏——栈（二）

前言

今天的笔记主要就是扩展一下昨天笔记的内容，让我们对于栈的操作的理解加深。同时还需要学会灵活应用栈来解决一些实际问题。最后还需要学习一个难度比较高的算法题目：单调栈，使用文字讲解有点难度，现在我会尝试使用属于我自己的方式把这个算法尽可能可以以动画的形式展现出来，如实在有困难，就直接联系本人吧。

一、后缀表达式（简单+）

前言

大家可以通过下面这道题目大概了解一下后缀表达式是什么

后缀表达式的计算原理规则：

从左到右遍历表达式的每个数字和符号，遇到的是数字就进栈，遇到的是符号，就将栈顶的两个数字依次出栈，进行运算（运算规则：后出栈的数字1 符号后出栈的数字2 ），再将运算结果进栈，知道获得最终结果。

样例：

后缀表达式例子：9 3 1 - 3 * + 10 2 / +

计算过程：

数字9入栈
数字3入栈
数字1入栈
遇到了 - 运算符，，这时候计算 3 - 1 = 2（注意数字的顺序，谁是减数，谁是被减数），数字2入栈
数字3入栈
遇到了运算符 * 。计算 2 * 3 = 6 ，数字6入栈
遇到了运算符 + 。9 + 6 = 15 .数字15入栈
数字10入栈
数字2入栈
遇到了运算符 / 。计算10 / 2 = 5，数字5入栈
遇到了运算符 + 。计算15 + 5 = 20.入栈。到这时遍历结束。最后栈中剩余一个数字20.

输入样例

1	`9 3 1 - 3 * + 10 2 / +`

输出样例

思路

无

代码

答案（请自己先思考一下再参考）

        
#include< iostream>
#include< string>
#include< stack>
using namespace std;
//后缀表达式计算函数
double calculate(const string str)
{
    stack< double> mystack;//用来存数据
    string Empty = " ";
    string ch = "+-*/";
    string numbers = "0123456789";
    string s = "0123456789+-*/";
    int start, end;
    double num, secnodnum, firstnum;
    for (int i = 0; i < str.length(); )
    {
        start = str.find_first_of(s, i);//查找第一个数字或者运算符
        end = str.find_first_of(Empty, i);//查找第一空格
        if (end == -1)//处理最后一个符号后没有空格的问题
        {
            end = str.length();
        }
        string tempstr = str.substr(start, end - start);//取出这一个元素
        if ((tempstr == "+") || (tempstr == "-") || (tempstr == "*") || (tempstr == "/"))
        {
            secnodnum = mystack.top();//取出栈顶元素
            mystack.pop();//出栈
            firstnum = mystack.top();//取出栈顶元素
            mystack.pop();//出栈
            if (tempstr == "+")
            {
                num = firstnum + secnodnum;
                mystack.push(num);
            }
            if (tempstr == "-")
            {
                num = firstnum - secnodnum;
                mystack.push(num);
            }
            if (tempstr == "*")
            {
                num = firstnum * secnodnum;
                mystack.push(num);
            }
            if (tempstr == "/")
            {
                num = firstnum / secnodnum;
                mystack.push(num);
            }
        }
        else
        {
            double temp = stod(tempstr);
            mystack.push(temp);
        }
        i = end + 1;//控制下标的移动
    }
    return mystack.top();
}
int main()
{
    string str;
    getline(cin, str);
    double ans = calculate(str);//记录后缀表达式运算的结果
    cout << ans << endl;
    return 0;
}

二、单调栈（中等-）

给定一个长度为 N的整数数列，输出每个数左边第一个比它小的数，如果不存在则输出 −1。

输入格式

第一行包含整数 N，表示数列长度。

第二行包含 N个整数，表示整数数列。

输出格式

共一行，包含 N个整数，其中第 i个数表示第 i个数的左边第一个比它小的数，如果不存在则输出 −1。

数据范围

$$
1≤N≤10^5\
1≤数列中元素≤10^9
$$

输入样例：

1 2	`5 3 4 2 7 5`

输出样例：

1	`-1 3 -1 2 2`

思路（！！！）

思路（请自己先思考一下再参考）

                                        知道一个原理
        从左往右寻找每个数的左边第一个比它自己小的数，是不是就意味着当前比遍历到的这个数左边一个数的左边的数
        （这里有点拗口，比如5 4 3，这里就是指4左边的数）要大的数，就绝对不可能找到，比如5 4 3,3前面为4,4前面为5，4<5，
        那么你在寻找比3第一个小的数的时候就不可能去找5了对不对,因为4都不可以了，比4大的就更不可能是了，
        我们代码中的数组st[] 存储的就是对当前遍历的数而言，对前面遍历过的数可能为比它小的数的集合，同时这个集合
        还是从0往tt优先级越来越高的，下标越大，越先被遍历到 。下面的图像就是对于样例的折线图的动画。

动画1

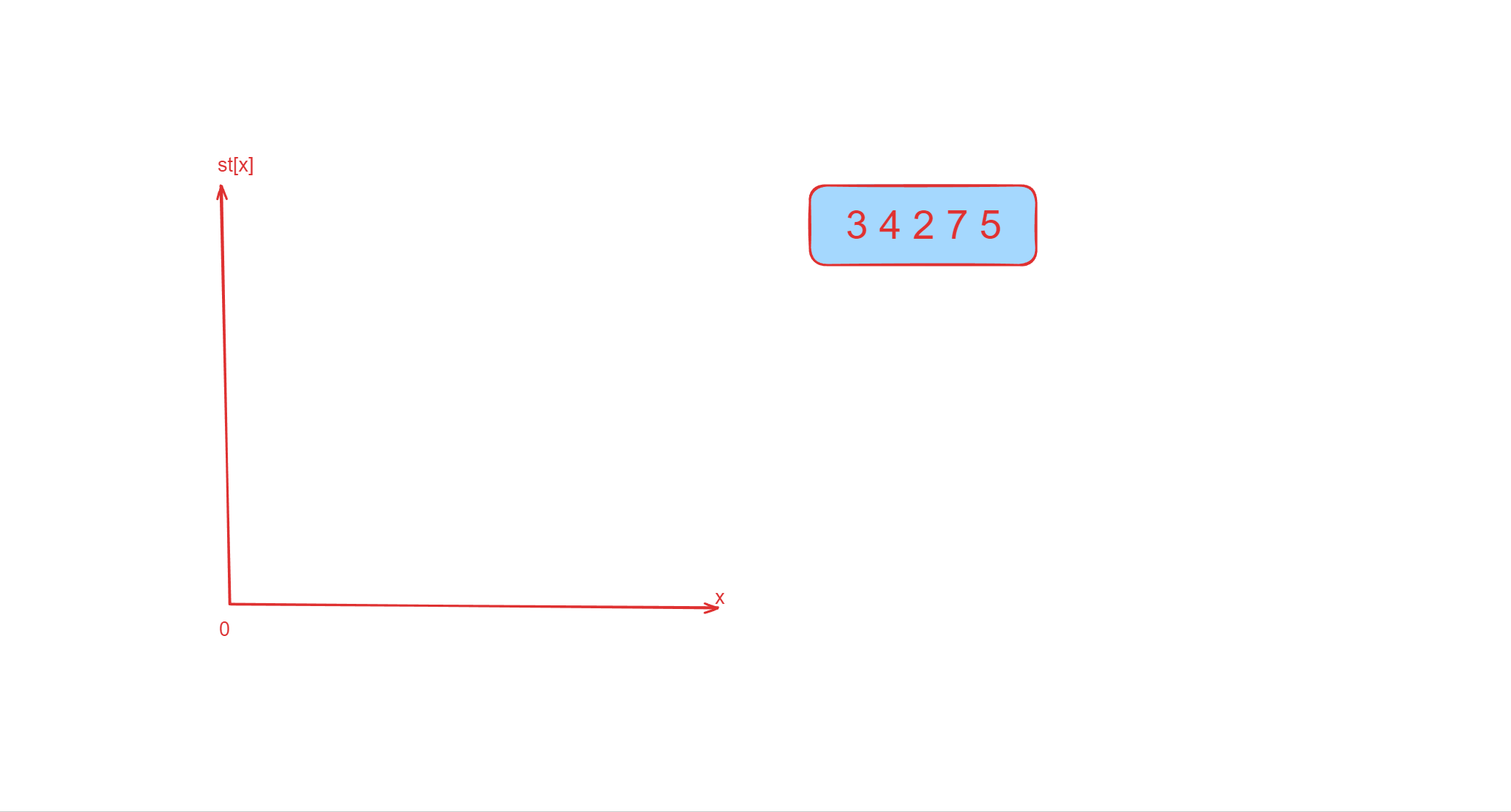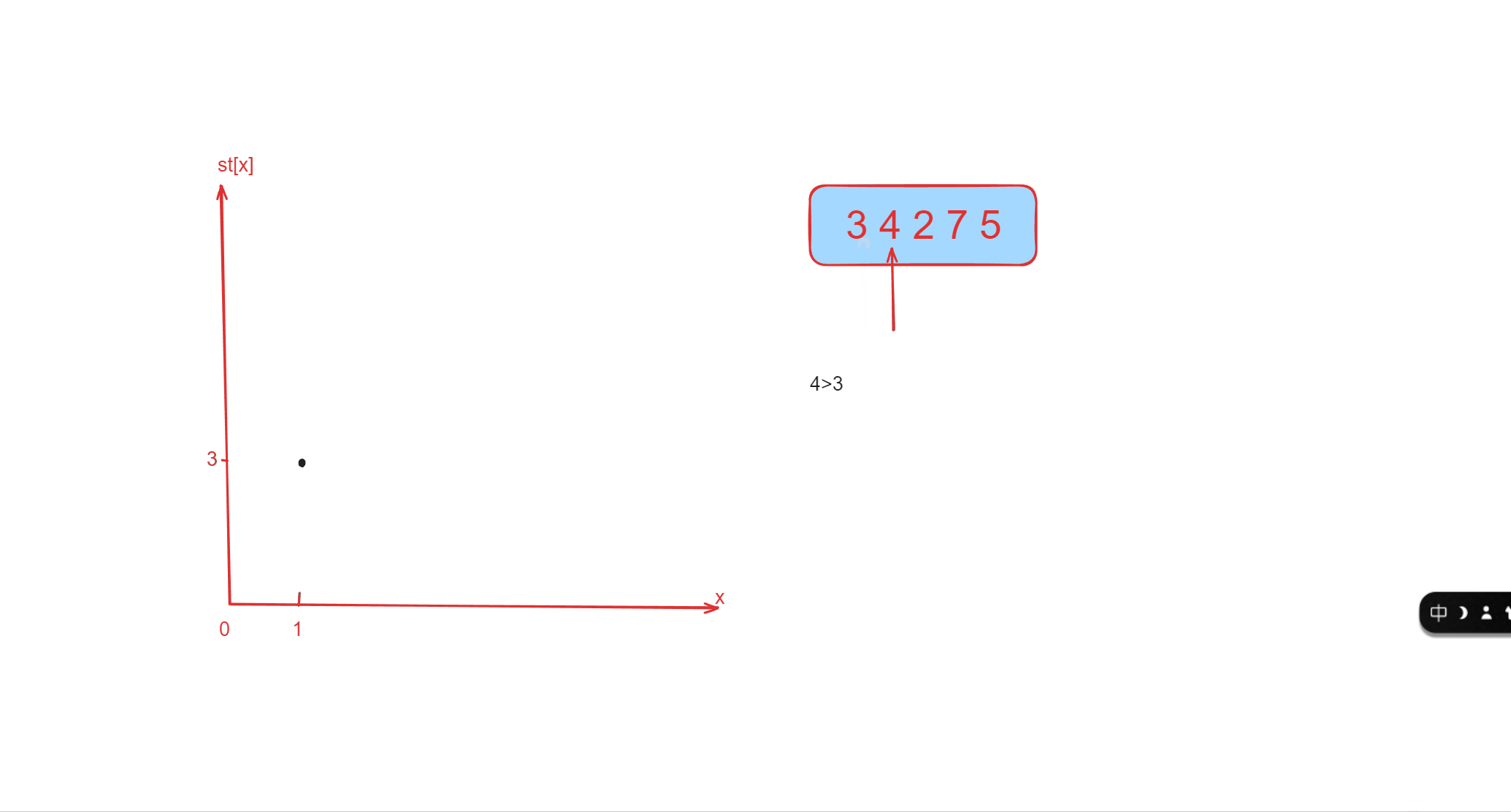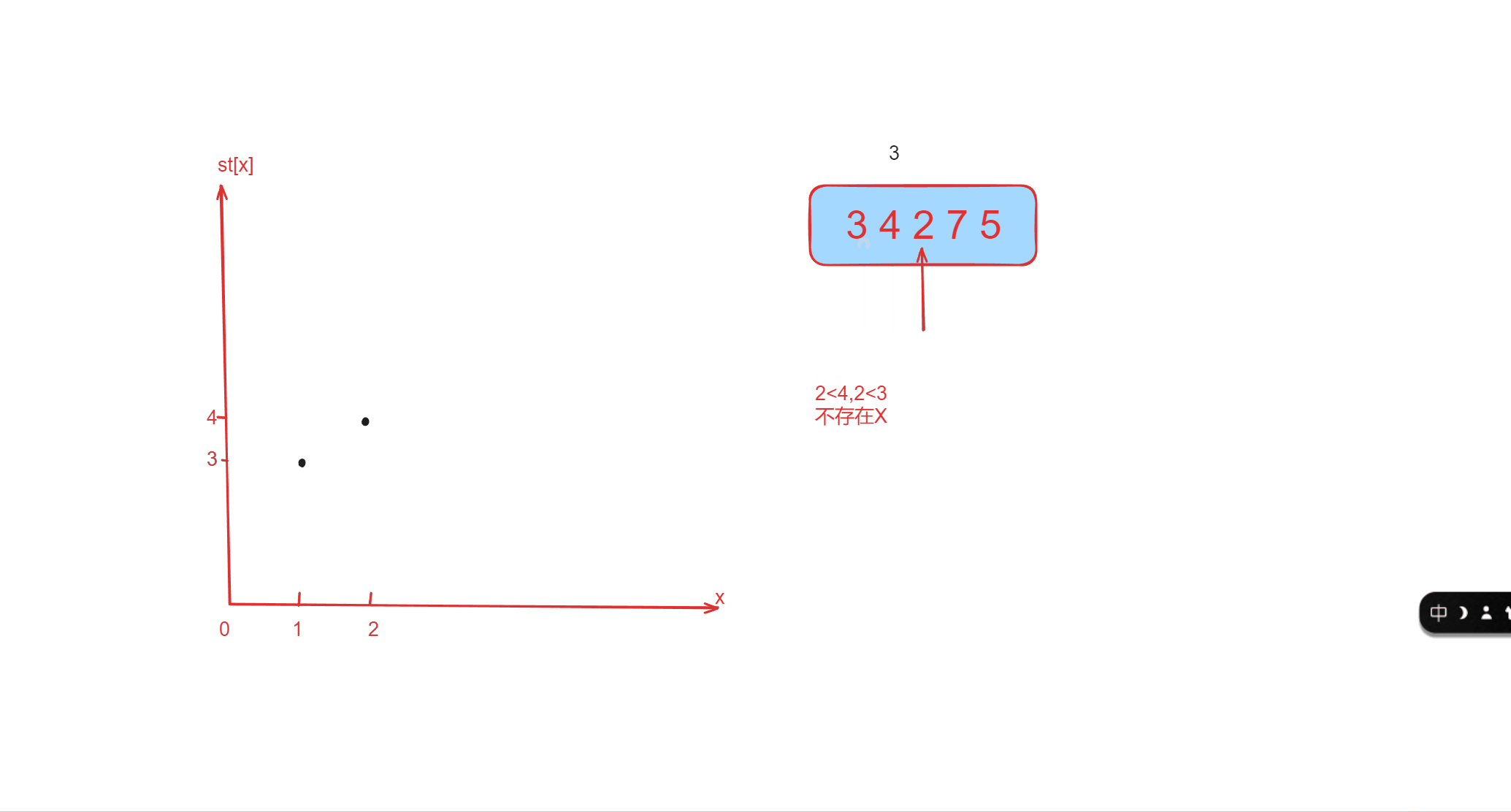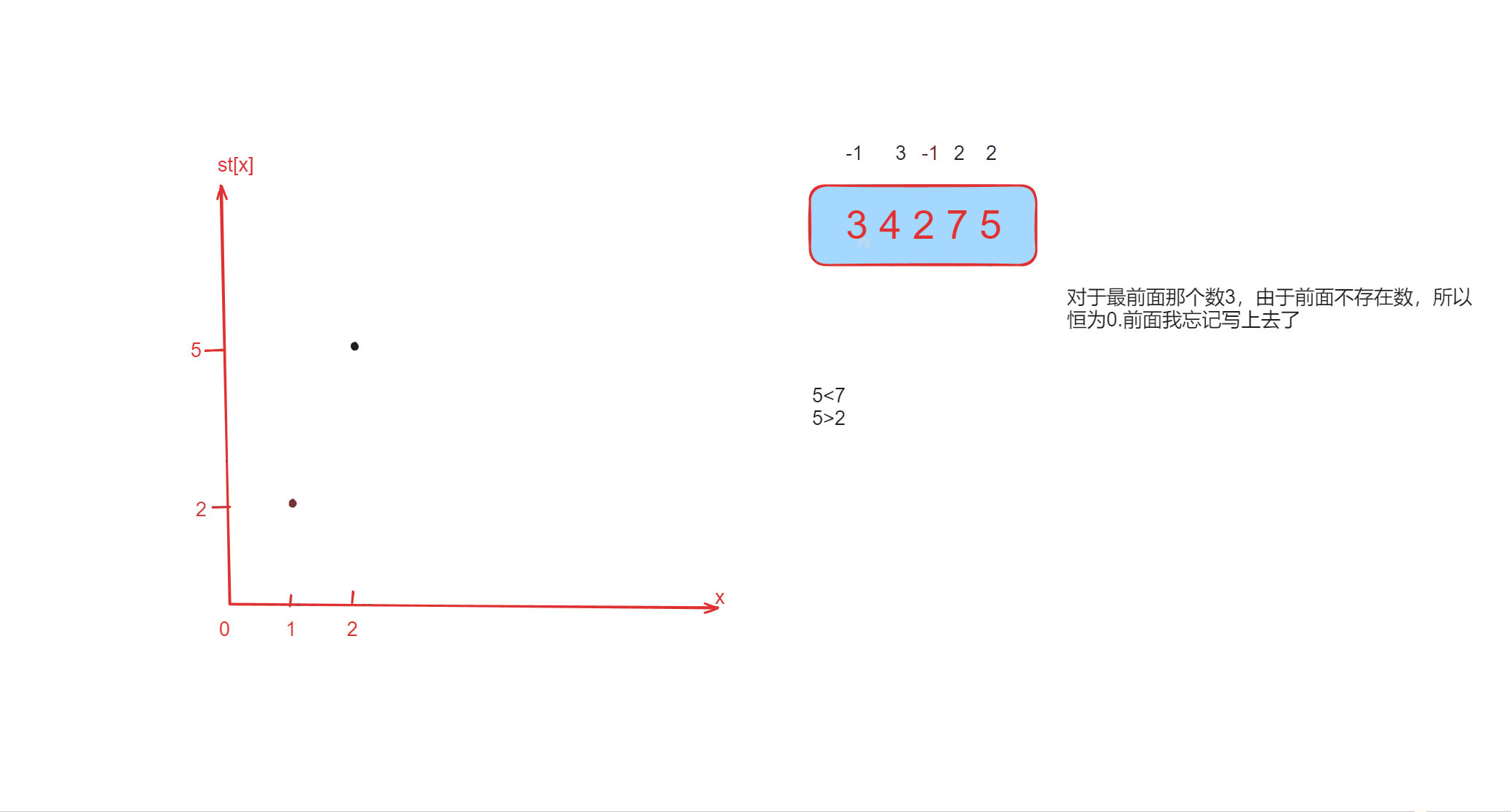
代码

答案（请自己先思考一下再参考）

        
#include < iostream>
#include < algorithm>
using namespace std;
const int N = 1e5 + 10;
int st[N];
int n;
int main()
{
    ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
    cin >> n;
    int tt = 0;
    for (int i = 1; i <= n; i++) {
        int x;
        cin >> x;
        while (tt && st[tt] >= x) tt--;
        if (tt) cout << st[tt] << " ";
        else cout << "-1 ";
        st[++tt] = x;
    }
    return 0;
}

算法练习专栏——队列+单调队列上一篇

算法学习专栏——栈（一）下一篇