算法学习专栏——二分法

一、数的范围（简单）

给定一个按照升序排列的长度为 n 的整数数组，以及 q 个查询。

对于每个查询，返回一个元素 k 的起始位置和终止位置（位置从 00 开始计数）。

如果数组中不存在该元素，则返回 -1 -1。

输入格式

第一行包含整数 n 和 q，表示数组长度和询问个数。

第二行包含 n 个整数（均在 1∼10000 范围内），表示完整数组。

接下来 q 行，每行包含一个整数 k，表示一个询问元素。

输出格式

共 q 行，每行包含两个整数，表示所求元素的起始位置和终止位置。

如果数组中不存在该元素，则返回 -1 -1。

数据范围

1≤n≤100000
1≤q≤10000
1≤k≤10000

输入样例：

6 3
1 2 2 3 3 4
3
4
5

输出样例：

1
2
3

3 4
5 5
-1 -1

思路

直播（录播）

方法一（铁对）

答案（请自己先思考一下再参考）

        
#include < iostream>
using namespace std;
const int N = 1e6 + 10;
int arr[N];
int main()
{
    int n,m;
    cin >> n >> m;
    for (int i = 0; i < n; i++) scanf("%d ",&arr[i]);
    while (m--)
    {
        int x;
        scanf("%d",&x);
        int l = 0, r = n - 1;
        while (l < r)
        {
            int mid = (l + r) / 2;
            if (arr[mid] >= x) r = mid;
            else l = mid + 1;
        }
        if (arr[l] != x) cout << "-1 -1" << endl;
        else
        {
            printf("%d ",l);
            int l = 0,r = n - 1;
            while (l < r)
            {
                int mid =(l + r + 1) / 2;
                if (arr[mid] <= x) l = mid;
                else r = mid - 1;
            }
            printf("%d\n",l);
        }
    }   
    return 0;
}

方法二（目前没有发现特殊情况）

答案（请自己先思考一下再参考）

        
#include < iostream>
#include < algorithm>
using namespace std;
const int N = 1e5 + 10;
int n;
int a[N];
int main() 
{
    ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
    int n, m;
    cin >> n >> m;
    for (int i = 0; i < n; i++) {
        cin >> a[i];
    }
    while (m--){
        int x;
        cin >> x;
        int l = -1, r = n;
        while (l + 1!= r) {
            int mid = l + r >> 1;
            if (x > a[mid]) l = mid;
            else r = mid;
        }
        if (r == n || a[r] != x)
        {
            cout << "-1 -1\n";
            continue;
        } 
        cout << r << " ";
        l = -1, r = n;
        while (l + 1!= r) {
            int mid = l + r >> 1;
            if (x < a[mid]) r = mid;
            else l = mid;
        }
        cout << l << '\n';
    }
    return 0;
}

二、冶炼金属（简单++）

小蓝有一个神奇的炉子用于将普通金属 O 冶炼成为一种特殊金属 X。

这个炉子有一个称作转换率的属性 V，V 是一个正整数，这意味着消耗 V 个普通金属 O 恰好可以冶炼出一个特殊金属 X，当普通金属 O 的数目不足 V 时，无法继续冶炼。

现在给出了 N 条冶炼记录，每条记录中包含两个整数 A 和 B，这表示本次投入了 A 个普通金属 O，最终冶炼出了 B 个特殊金属 X。

每条记录都是独立的，这意味着上一次没消耗完的普通金属 O 不会累加到下一次的冶炼当中。

根据这 N 条冶炼记录，请你推测出转换率 V 的最小值和最大值分别可能是多少，题目保证评测数据不存在无解的情况。

输入格式

第一行一个整数 N，表示冶炼记录的数目。

接下来输入 N 行，每行两个整数 A、B、，含义如题目所述。

输出格式

输出两个整数，分别表示 V 可能的最小值和最大值，中间用空格分开。

数据范围

对于 30% 的评测用例，1≤N≤10^2^
对于 60% 的评测用例，1≤N≤10^3^
对于 100% 的评测用例，1≤N≤10^4^，1≤B≤A≤10^9^

输入样例：

输出样例：

20 25

样例解释

当 V=20=20 时，有：⌊75/20⌋=3，⌊53/20⌋=2，⌊59/20⌋=2，可以看到符合所有冶炼记录。

当 V=25=25 时，有：⌊75/25⌋=3，⌊53/25⌋=2，⌊59/25⌋=2，可以看到符合所有冶炼记录。

且再也找不到比 20 更小或者比 25 更大的符合条件的 V 值了。

思路

方法一 就不介绍了，就是最基本的二分思路，两个模板。

方法二 主要是按照数学公式推导的方法来写的，推到过程如下：

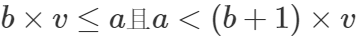
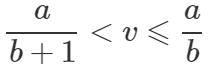
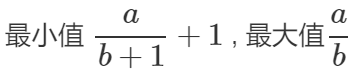
代码

方法一

答案（请自己先思考一下再参考）

        
#include < iostream>
using namespace std;
int N,x,y,Max = 1e9;
const int n = 10010;
int arr[n],ans[n];
int check(int x)
{
    for (int i = 0; i < N; i ++ ) 
    {
        if(ans[i] < arr[i] / x) 
            return 2;
        if (ans[i] > arr[i] / x)
            return 3;
    }
    return 1;
}
int main()
{
    cin >> N;
    for (int i = 0; i < N; i++) cin >> arr[i] >> ans[i];
    int left = 1,right = Max;
    while(left < right)
    {
        int  mid = (left + right) >> 1;
        if (check(mid) == 1 || check(mid) == 3) right = mid;
        else left = mid + 1;
    }
    cout << left << " ";
    left = 1;
    right = Max;
    while(left < right)
    {
        int  mid = (left + right + 1) >> 1;
        if (check(mid) == 2 || check(mid) == 1) left = mid;
        else right = mid - 1;
    }
    cout << left;
    return 0;
}

方法二

答案（请自己先思考一下再参考）

        
#include < iostream>
using namespace std;
int main()
{
    long long n = 0,a,b,c=0x3f3f3f3f,d=0;
    cin >> n;
    while (n -- )
    {
        cin >> a >> b;
        c = min(c,a/b);
        d = max(d,a/(b+1) + 1);
    }
    cout << d << " " << c;
    return 0;
}

三、牛可乐和魔法封印(扩充)

链接

牛可乐得到了一个长度为 nnn 且非严格单调递增的序列 aaa，然而这个序列被 qqq 层魔法封印了，其中第 iii 层封印的问题包含两个整数 xi,yi(xi≤yi)x_i,y_i(x_i\leq y_i)xi,yi(xi≤yi)，牛可乐必须正确回答序列中大于等于 xix_ixi且小于等于 yiy_iyi 的数字个数才能够解开该层封印。

牛可乐觉得这个问题太难了，于是他想请你帮助他解开序列的 qqq 层封印。

输入描述:

$$
第一行包含一个整数 n(1≤n≤10^5)，表示序列的长度。\

第二行包含 n 个整数，其中 −10^9≤a_i≤10^9\

第三行包含一个整数 q(1≤q≤10^5)，代表封印层数。\

之后 q 行，每行两个整数 x_i,y_i(-10^9\leq x_i\leq y_i\leq 10^9)，代表该层封印的询问。
$$

输出描述:

$$
对于每层封印，输出一行一个整数，代表在范围内的数字个数。
$$

输入

复制

输出

复制

1
2
3

4
5
1

说明

对于第一层封印，2,3,4,52,3,4,52,3,4,5在范围内，答案为 444。

对于第二层封印，1,2,3,4,51,2,3,4,51,2,3,4,5在范围内，答案为 555。

对于第三层封印，333在范围内，答案为 111。

示例2

输入

复制

输出

复制

1
2
3

2
3
5

代码

答案（请自己先思考一下再参考）

        
#include < iostream>
#include < algorithm>
using namespace std;
const int N = 1e5 + 10;
int n, q;
int a[N];
int main()
{
    ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
    }
    cin >> q;
    while (q--) {
        int x, y;
        cin >> x >> y;
        int l = 1, r = n + 1;
        while (l < r) {
            int mid = l + r >> 1;
            if (a[mid] >= x) r = mid;
            else l = mid + 1;
        }
        int ll = 0, rr = n;
        while (ll < rr) {
            int mid = (ll + rr + 1) >> 1;
            if (a[mid] <= y) ll = mid;
            else rr = mid - 1;
        }      
        cout << rr - l + 1 << '\n';
    }  
    return 0;
}

2、数据结构——简单的线性表——顺序表（一）上一篇

算法学习专栏——排序算法（二）下一篇