算法学习专栏——Tire算法

前言：字典树（Tire）

定义

Tire是一种能够快速插入和查询字符串的多叉树结构

根结点编号为0，初始位置，不存任何东西。

其他节点：

1.标记路径

2.记录单词插入次数

边：表示字符

Tire维护字符串集合，支持两种操作

*void insert(char s): 向集合插入一个字符串

*void query(char s): 在集合中查询一个字符串

建字典树

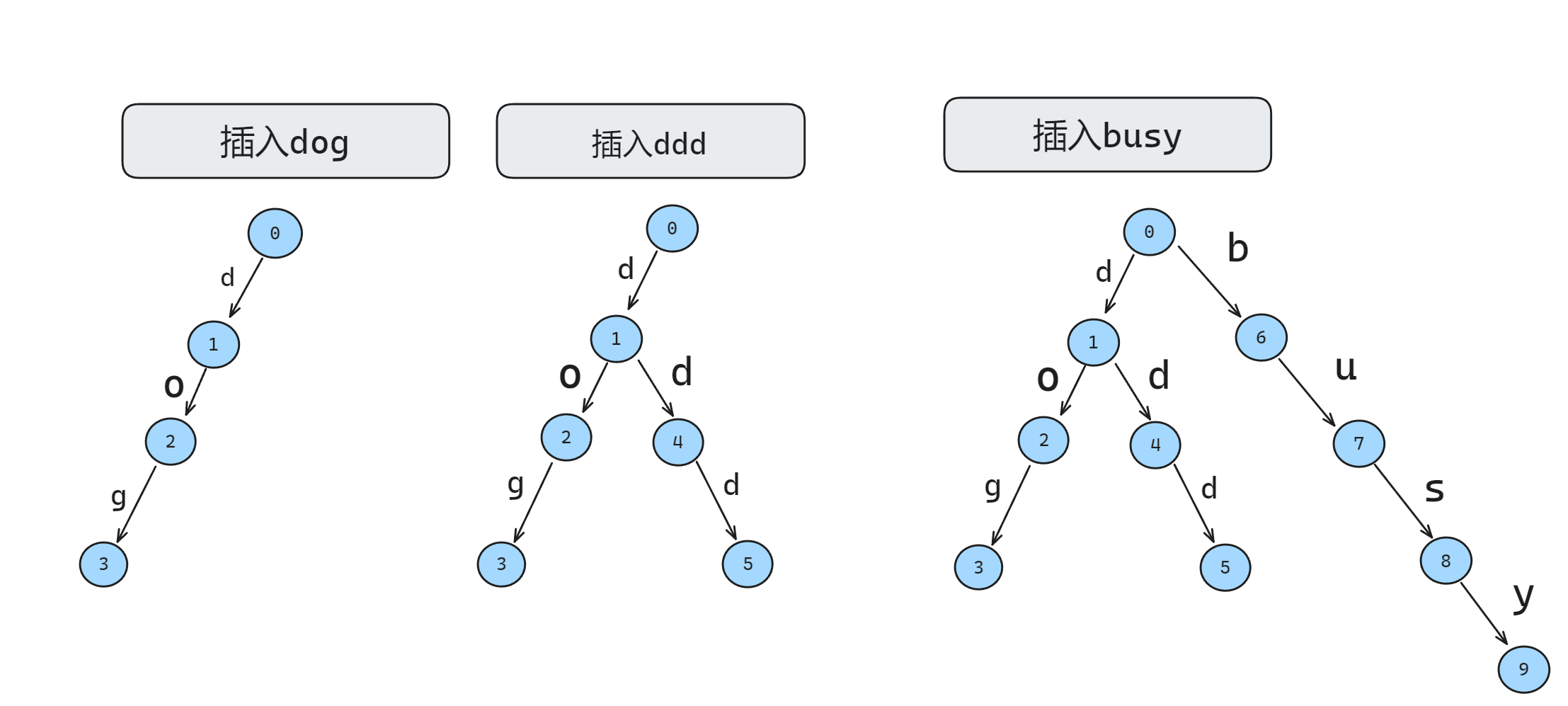
下面我们就可以准备代码编写需要的数组了：

节点编号idx:

用来记录节点
儿子数组 son[p] [i]:

存储从节点p沿着这条边走到的子节点编号，比如上图的节点1，对应表示的就是从1节点沿着d边可以走到节点4。

而这里的边(i)为26个字符**(a~~z)对应的映射值0~~25，每个节点最多可以有26个分支，例如上面图中的：son[0] [3] = 1;son[1] [14] = 2;son[1] [3] = 4……**
记录数组:

存储的是以当前节点p为结尾的插入字符串个数

插入操作

1.空 Tire 仅有1个根结点，编号为0 ；

2.从根开始插，枚举字符串的每个字符，如果有儿子（也就是子节点），则p指针走到儿子如果没有儿子，则先创建儿子，p指针再走到儿子；反之则直接走向儿子

3.在单词结束点记录插入次数，也就是cnt[p]++

#include <iostream>
#include <algorithm>

using namespace std;
const int N = 1e5 + 10;
int son[N][26];
char s[N];
int cnt[N];
int n, idx;

void insert(char s[]) {
    int p = 0;
    for (int i = 0; s[i]; i++) {
        int u = s[i] - 'a';
        if (!son[p][u]) son[p][u] = ++idx;
        p = son[p][u];
    }
    cnt[p] ++;
}

查询操作

1.从根开始查，扫描字符串

2.有字母**s[i]**，则走下去，能走到词尾，则返回插入次数

3.无字母s[i],则返回0

int query(char s[]) {
    int p = 0;
    for (int i = 0; s[i]; i++) {
        int u = s[i] - 'a';
        if (!son[p][u]) return 0;
        p = son[p][u];
    }
    return cnt[p];
}

一、Tire字符串统计（简单+）

维护一个字符串集合，支持两种操作：

I x 向集合中插入一个字符串 x；
Q x 询问一个字符串在集合中出现了多少次。

共有 N 个操作，所有输入的字符串总长度不超过 10^5^，字符串仅包含小写英文字母。

输入格式

第一行包含整数 N，表示操作数。

接下来 N 行，每行包含一个操作指令，指令为 I x 或 Q x 中的一种。

输出格式

对于每个询问指令 Q x，都要输出一个整数作为结果，表示 x 在集合中出现的次数。

每个结果占一行。

数据范围

1≤N≤2∗104

输入样例：

5
I abc
Q abc
Q ab
I ab
Q ab

输出样例：

1
2
3

1
0
1

思路

直播讲解（会录屏）

代码

答案（请自己先思考一下再参考）

        
#include < iostream>
#include < algorithm>
using namespace std;
const int N = 1e5 + 10;
int a[N][26];
char s[N];
int cnt[N];
int n, idx;
void insert(char s[]) {
    int p = 0;
    for (int i = 0; s[i]; i++) {
        int u = s[i] - 'a';
        if (!a[p][u]) a[p][u] = ++idx;
        p = a[p][u];
    }
    cnt[p] ++;
}
int query(char s[]) {
    int p = 0;
    for (int i = 0; s[i]; i++) {
        int u = s[i] - 'a';
        if (!a[p][u]) return 0;
        p = a[p][u];
    }
    return cnt[p];
}
int main() 
{
    ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
    cin >> n;
    for (int i = 0; i < n; i++) {
        char op[2];
        cin >> op >> s;
        if (op[0] == 'I') {
            insert(s);        
        } else {
            cout << query(s) << '\n';
        }
    }  
    return 0;
}

二、最大异或对（简单++）

在给定的 N 个整数 A1，A2……AN 中选出两个进行 xor（异或）运算，得到的结果最大是多少？

输入格式

第一行输入一个整数 N。

第二行输入 N 个整数 A1～AN。

输出格式

输出一个整数表示答案。

数据范围

1 ≤N ≤10^5^
0 ≤Ai <2^31^

输入样例：

1
2

3
1 2 3

输出样例：

思路

直播讲解（录屏）

代码

#include < iostream>
#include < algorithm>
using namespace std;
const int N = 1e5 + 10, M = N * 31;
int a[M][2], b[N];
int n,idx;
long long ans;
void insert(int x) {
    int p = 0;
    for (int i = 30; i >= 0; i--) {
        int u = x >> i & 1; // 取出二进制的第i个数，这里需要从高位开始，因为我们找的数越大肯定要找高位优先为1的数
        if (!a[p][u]) a[p][u] = ++idx;
        p = a[p][u];
    }
}
long long query(int x){
    long long p = 0, res = 0;
    for (int i = 30; i >= 0; i--) {
        int u = x >> i & 1;
        if (a[p][!u]) { // p结点一共就两个儿子
            p = a[p][!u];//因为从高到低枚举，~高位的值一定是大的
            res = res * 2 + 1; // 累加
        } else {
            p = a[p][u];
            res = res * 2;
        }
    }    
    return res;
}
int main()
{
    ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
    cin >> n;
    for (int i = 0; i < n; i++) {
        cin >> b[i];
        insert(b[i]);
    }
    for (int i = 0; i < n;i++) {
        long long k = query(b[i]);
        ans = max(ans, k);        
    }    
    cout << ans;
    return 0; 
}

算法学习专栏——排序算法（一）上一篇

算法学习专栏——单调队列+优先队列下一篇