一、线性表的基本概念
严谨定义
线性表是具有相同数据类型的n(n≥0)个数据元素的有限序列,其中n为表长,当n=0时线性表是一个空表。若用L命名线性表,则其一般表示为
$$
L=(a1,a2,…,aiai+1…,an)
$$

专业概念
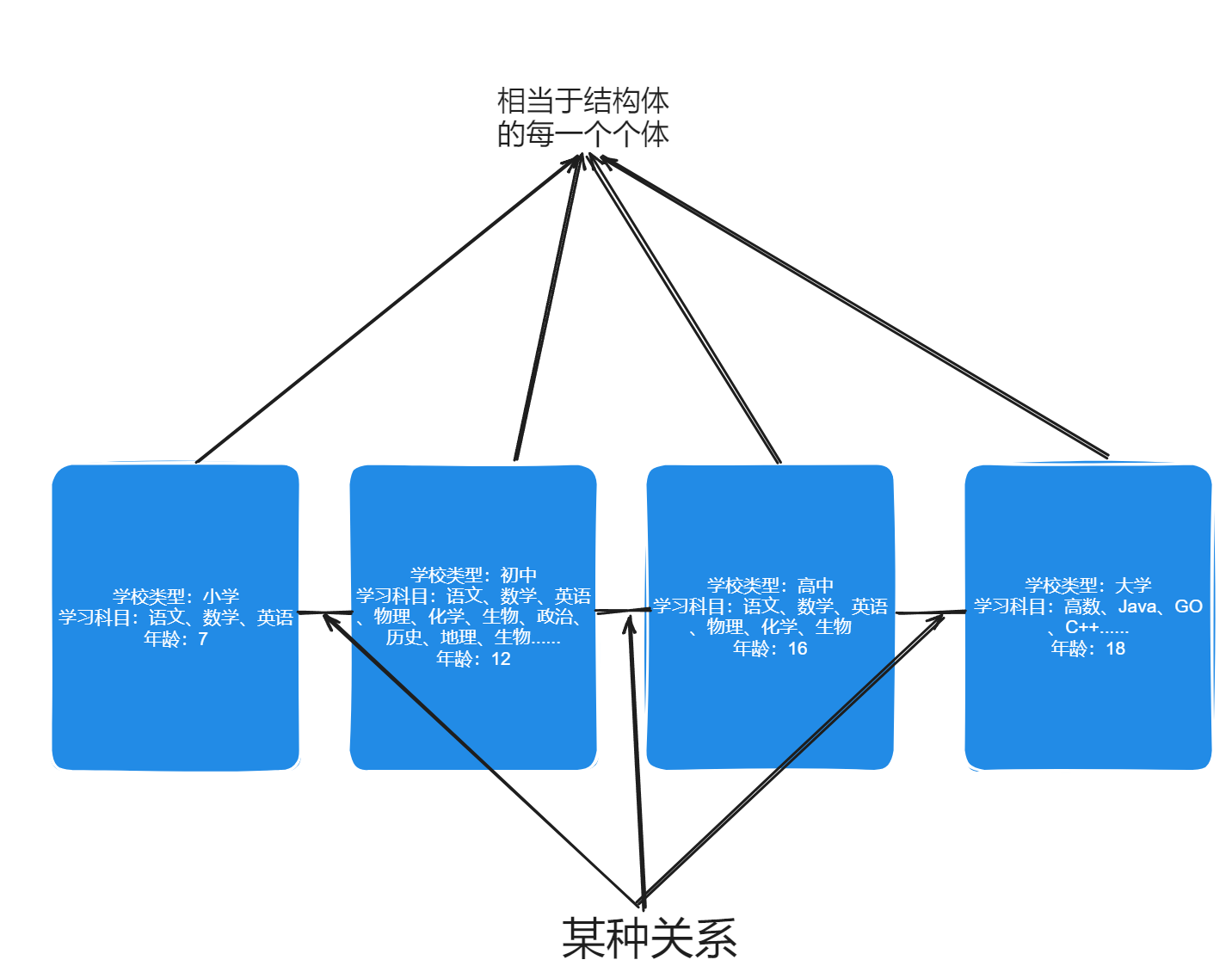
二、理解到底什么是线性表
实际上线性表使用大白话来讲,可以理解为:将一组一组数据按照一定的关系联系起来的结构。例子
三、线性表的基本操作(实际上之后我们介绍的每一种结构都是按照这种思路进行分析学习的)
初始化操作(InitList(&L))
销毁操作(DestoryList(&L))
插入操作(ListInsert(&L,i,e))
删除操作(ListDelete(&L,i,&e))
按值查找(LocateElem(L,.e))
按位置查找(GetElem(L,i))
求线性表长(Length(L))
输出线性表所有元素
判断表是否为空
补充知识
&这个符号的含义: 就是将参数修改的结果带回来。换句话说就是你给函数传了一个X,函数内部对X的处理会真正影响到函数外的X的数值,比如你调用一个函数实现X+1操作,那么你的原本数据也会随之加1.
接下来我们就会讲解线性表的具体类型已经如何结合结构体来实现这种关系……
四、顺序表
定义
用顺序存储的方式实现线性表顺序存储。把逻辑上相邻的元素存储在物理位置上也相邻的存储单元中,元素之间的关系由存储单元的邻接关系来体现。线性表是具有相同数据类型的所占空间大小也相同的n**(n≥0)**个数据元素的有限序列。
结构体定义
1
2
3
4
5
6
7
8
9
10
11
12
| typedef int Elemtype;
#define MaxSize 10
typedef struct{
ElemType data[MaxSize];
int length;
}SqList;
typedef struct{
int *data;
int MaxSize;
int length;
}SqList;
|
对于动态存储的data的理解: 假设我们为p分配了40个字节的空间,由于1个int类型数据占4个字节,因此我们就可以为p分配10个int类型的数据,地址是从2000~2040(这个2000是我假设的指针p的第一个元素起始位置)

实现功能一:初始化一个顺序表(完整代码)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
|
#include <stdio.h>
typedef int Elemtype;
#define MaxSize 10;
typedef struct{
ElemType data[MaxSize];
int length;
}SqList;
void InitList(SqList &L) {
for (int i = 0; i < MaxSize; i ++) {
L.data[i] = 0;
}
L.length=o;
}
int main() {
SqList L;
InitList(L);
return 0;
}
#include <stdio.h>
#include <stdilb.h>
typedef int Elemtype;
#define InitSize 10;
typedef struct{
int *data;
int MaxSize;
int length;
}SqList;
void InitList(SqList &L) {
L.data=(int *)malloc(sizeof(int) * InitSize);
L.length=0;
L.MaxSize=InitSize;
}
void InsertSqlist(Sqlist &L,int len) {
int *p = L.data;
L.data=(int *)malloc((L.MaxSize + len)*sizeof(int));
for (int i = 0; i < L.length; i++) {
L.data[i] = p[i];
}
L.MaxSize = L,MaxSize + len;
free(p);
}
int main() {
SqList L;
InitList(L);
InsertSqlist(L,5);
return 0;
}
|
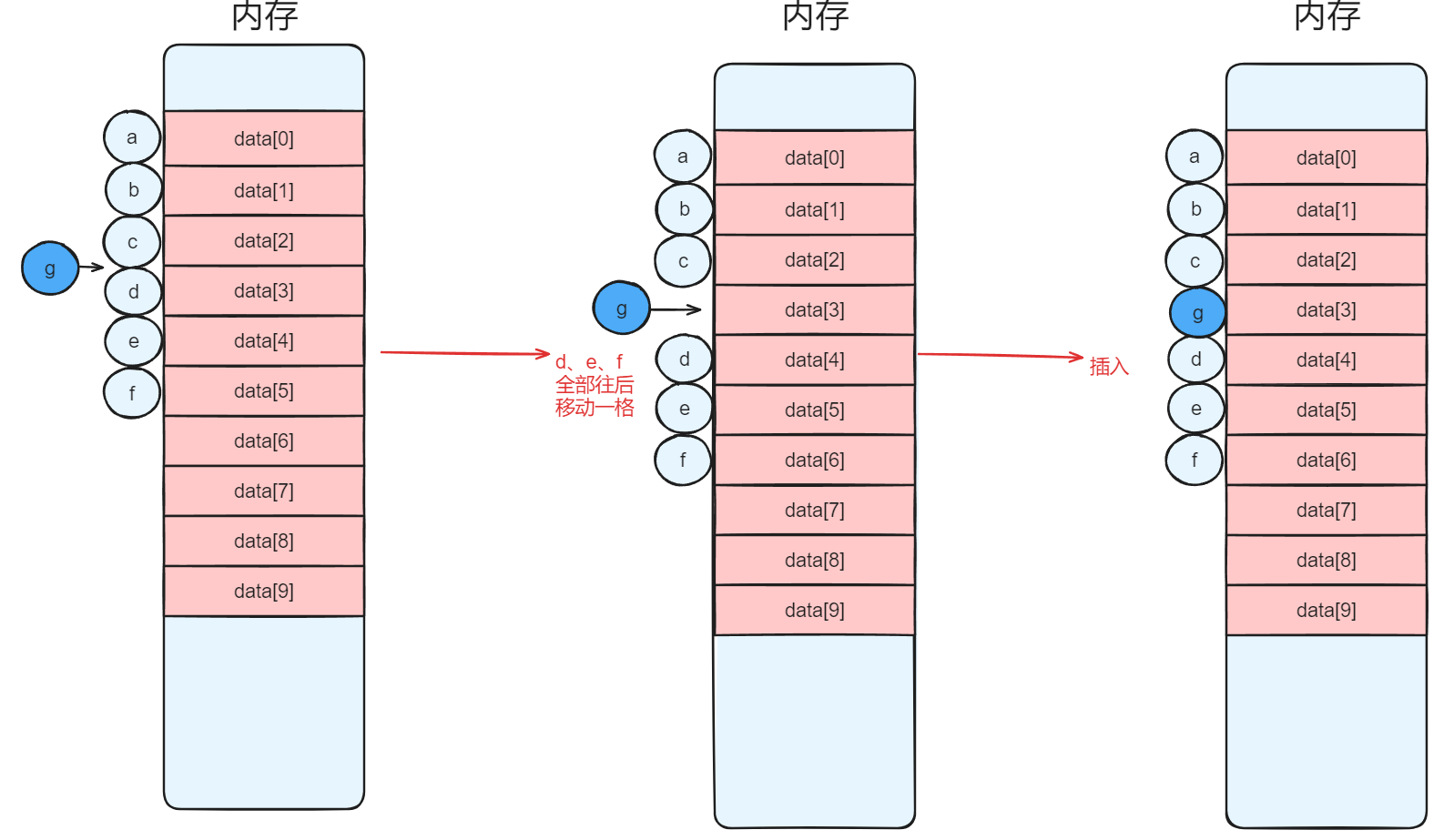
实现功能二:插入元素

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
|
void ListInsert(Sqlist &L,int i,int e) {
for (int j=L.length;j >= i; j--) {1
L.data[j] = L.data[j - 1];
}
L.data[i - 1] = e;
L.length++;
}
int main() {
Sqlist L;
InitList(L);
ListInsert(L,1,1);
ListInsert(L,2,2);
ListInsert(L,3,3);
ListInsert(L,4,4);
ListInsert(L,5,5);
ListInsert(L,3,6);
return 0;
}
bool ListInsert(Sqlist &L,int i, int e) {
if (i < 1 || i > L.length + 1) return false;
if (L.length >= MaxSize) return false;
for (int j=L.length;j >= i; j--) {1
L.data[j] = L.data[j - 1];
}
L.data[i - 1] = e;
L.length++;
return true;
}
|
2.0是健壮的代码,可以应对特殊情况

时间复杂度
最好情况: 就是元素刚好插到顺序表尾部,这时就不需要移动元素,复杂度:O(1)
最坏情况: 就是元素插在顺序表的最前面,这时就需要将顺序表所有元素向后移动一个位置 复杂度:O(n)
平均情况: 新元素插入到任何一个位置的概率是相同的,为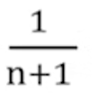 从
从i=1开始,循环n次;i=2时,循环n-1次;……i=n+1,循环0次。现在计算一下平均循环次数 = n*p + (n - 1) p …… 1 * p = p(1 + 2 + 3 + … + n) = p * n(n +1)/2=n/2
平均时间复杂度:O(n)
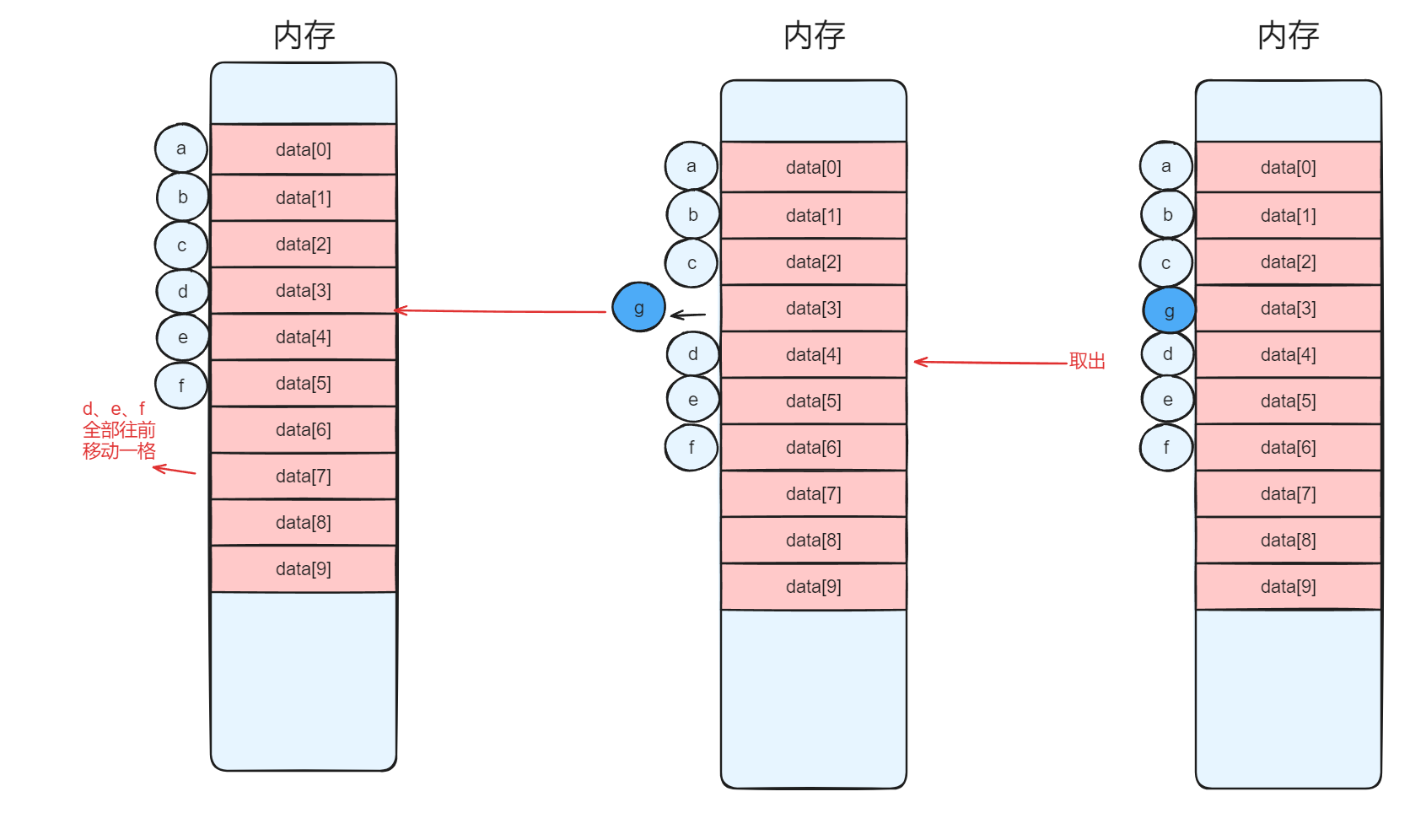
实现功能三:删除元素(其实和插入操作异曲同工)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
bool ListDelete(Sqlist &L,int i,int &e) {
if(i<1||i>L.length) return false
e = L.data[i - 1];
for (int j = i; j < L.length; j++) {
L.data[j - 1] = L.data[j];
}
L.length--;
return true;
}
int main() {
Sqlist L;
InitSqlist(L);
int e = -1;
if (ListDelete(L,3,e)) {
printf("删除第3个元素成功,第3个元素使%d",e);
} else {
printf("删除不合法!!!");
}
return 0;
}
|
时间复杂度
- 和插入操作是一模一样的,推理过程几乎都是一样的,所以这里就不重复介绍了……
实现功能三:按位置查找元素
1
2
3
4
5
|
ElemType GetElem(Sqlist L, int i) {
return L.data[i - 1];
}
|
时间复杂度:O(1)
实现功能四:按值查找
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
int GetByElem(Sqlist L,ElemType e) {
for (int i = 0;i < L.length; i++) {
if (L.data[i] == e) {
return i + 1;
}
}
return 0;
}
for (int i = 0;i < L.length; i++) {
if (L.data[i].a == e.a && L.data[i] == e.b && L.data[i].c == e.c) {
return i + 1;
}
}
return 0;
}
|
时间复杂度
和之前的插入、删除是一模一样的思路,此处不再讲解。
顺序表特点
- 随意访问,即可以在O(1)时间找到第i个元素
- 存储密度高,每个节点只存储数据元素
- 拓展容量不方便(即便使用动态分配的方式实现,时间复杂度也是很高的)
- 插入删除操作不方便,需要移动大量元素
注意事项
我们需要非常注意我们何时需要添加引用& ,何时不需要添加,加了之后,函数内部对元素的操作就会直接影响到传入的那个参数本身!!!
下一节内容是:3、简单的线性表——单链表!!!
一定要把本节内容看懂再往下看,不然会非常痛苦的哦o(╥﹏╥)oo(╥﹏╥)oo(╥﹏╥)o……..






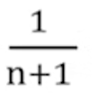 从
从