24、数据结构——二叉树——前中后序遍历

一、二叉树的遍历（理论部分）

本节我将给大家介绍三种遍历方式：

前序遍历（根左右）
中序遍历（左根右）
后序遍历（左右根）

现在我们就来稍微讲一下这三个遍历是咋遍历的，后面括号里的内容实际上就是遍历的规则，可以结合参考下面进行理解。

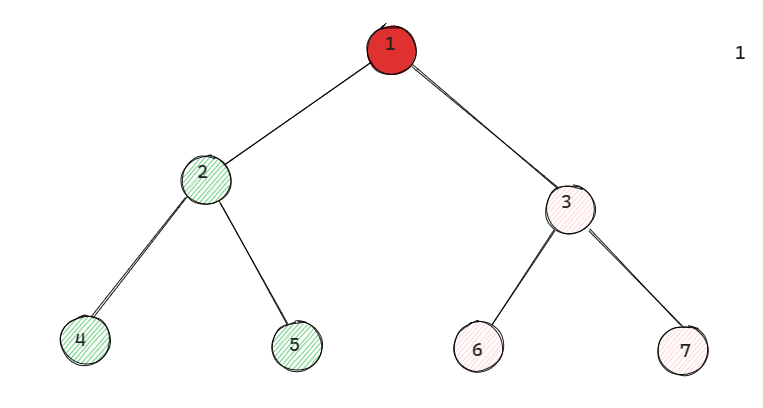
前序遍历（前根遍历）

以上图为例：

首先从根节点出发，始终按照根左右的口诀进行遍历，所以结点1的下一步应该是遍历到结点2，到结点2之后继续按照根左右的规则进行遍历就到了结点4，然后此时你会发现4没有左节点，然后又发现没有右节点，那么我们就回溯到4的父节点2，父节点2左节点刚刚已经找过一次了，现在就找右节点，也就是结点5，下面和节点4也是同样的道理会回到节点2，然后你发现节点2的左右结点都已经遍历过了，所以再回到节点2的父节点，也就是结点1.

然后节点1左节点遍历过了，所以进入右节点3，对于右节点3也是和节点2同样的规则，最后我们就可以得到这棵树的前序遍历： 1->2>4>5->4->3->6->7

中序遍历

如果前序遍历看懂了，那么下面两个遍历就简单一些了，和前序遍历的区别就是规则不同，对于中序遍历来说是按照左根右的规则遍历的。

首先，始终记住 左根右的规则 ，第一个遍历的是左节点，那么从根节点出发寻找左节点，那就是结点2，但是结点2现在在2、4、5这棵子树里不是左节点，而是根节点，因此我们要继续找这棵树的左节点，一直找下去，最后我们找到的左节点就是4，找完4左节点之后，再往上找根节点，也就是结点2，找完根节点了，就是时候找右节点了，也就是结点5，再回溯到节点2回溯到结点1，结点1是根节点因此下一步遍历到的就是节点1.右边也是一个道理。中序遍历就是： 4->2->5->1->6->3->7如果这里没有看懂的话，可以看下面的动画尝试理解：

后序遍历（后根遍历）

这个理解过程就交给大家自己了，下面我就直接来举几个例子来让大家看看是否对这三种遍历方式理解好了：

如果没有看明白，可以看看链接，讲解得十分清楚！前面6min是讲解这三种遍历方式部分，后面的部分基本都是练习题部分。

这一块内容大家必须理解程度100%，不然后面的内容就完全看不懂了的！！！

注意：对于这部分内容考研考到过

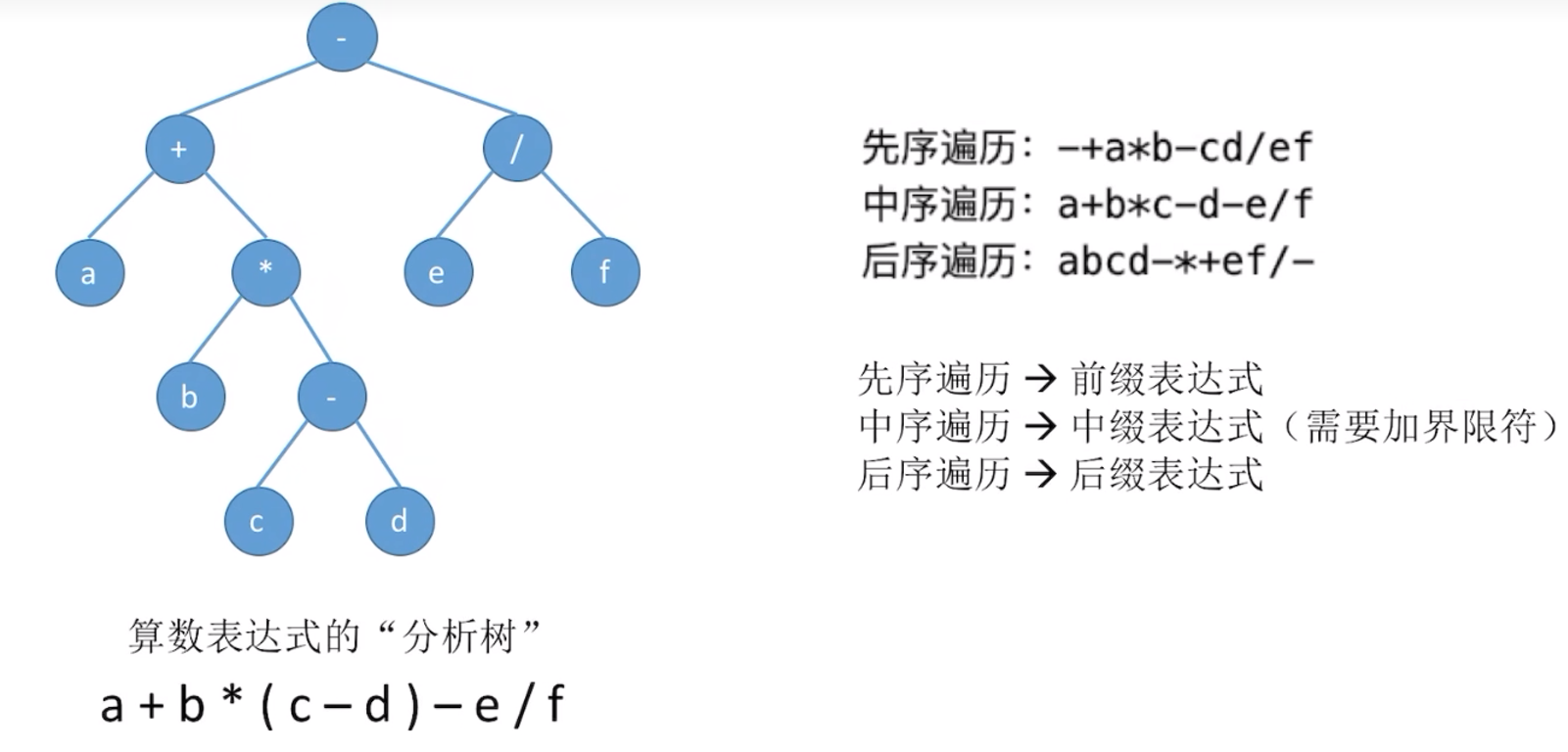
这个部分就开始递归方面内容的理解了，如果大家现在的目标是考研，那么这个地方的理解就必须是100%的，如果只是为了学完这个学期的数据结构的话，下面的代码部分就不用看了，后面再了解一下层次遍历是什么即可

二、三种遍历（代码）

结构体

typedef struct BitNode {
    ElemType data;
    struct BitNode *lchild, *rchild;
}BitNode, *BitTree;

先序遍历递归代码

void Visit(BitTree T) {
    // 这里面的代码就是随意了的，比如下面我写的就是打印一下这个节点的数据
    printf("%d ", T.data); // 假设data的类型是int
}
// 先序遍历
void PreOrder(BitTree T) {
    if (T != NULL) {
        Visit(T); // 访问根节点
        PreOrder(T -> lchild);  // 遍历左子树
        PreOrder(T -> rchild);  // 遍历右子树
		// 这个地方就看是递归层次代码的理解了，这个地方大家必须理解透彻的！！
    }
}

中序遍历递归代码

void Visit(BitTree T) {
    printf("%d ", T.data); 
}
// 中序遍历
void PostOrder(BitTree T) {
    if (T != NULL) {
        PostOrder(T -> lchild);  
        Visit(T); 
        PostOrder(T -> rchild);  
    }
}

后序遍历递归代码

void Visit(BitTree T) {
    printf("%d ", T.data); 
}
// 后序遍历
void BackOrder(BitTree T) {
    if (T != NULL) {
        BackOrder(T -> lchild);  
        BackOrder(T -> rchild);  
          Visit(T); 
    }
}

注意

对于王道视频中的通过遍历次数判断遍历顺序的办法本人还是不是非常建议，因为这种办法感觉还是会对于其本生的理解减弱，本人更加推崇使用三个原则的方法来进行遍历顺序的判断。

应用：求树的深度

int treeDepth(BitTree T) {
    if (T == NULL) {
        return 0;
    }
    else {
        int l = treeDepth(T->lchild);
        int r = treeDepth(T->rchild);
        return l>r?l + 1:r + 1;
    }
}

四、层次遍历（相比之下最简单）

规则就是一句话： 层数按照从小到大依次将各层元素从左到右连接出来即可，比如下图的层次遍历为：1->2>3->4->5->6->7

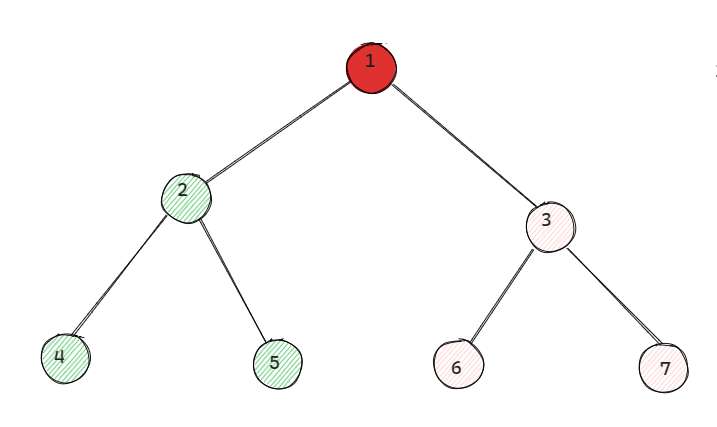
算法实现思想

初始化一个队列
根节点入队
若队列非空，则队头结点出队，访问该结点，并将其左右结点插入队尾（有的话）
重复第3步一直到队列为空为止

代码实现

typedef struct BiTNode {
    char data;
    struct BitNode * lchild, *rchild;
}BiTNode, *BiTree;

typedef struct LinkNode{
    BiTNode * data; // 注意：需要存的是指针而不是结点本身
    struct LinkNode *next;
}LinkNode;
void LevelOrder(BitNode T) {
    LinkQueue Q;
    InitQueue(Q);
    BitTree p;
    EnQueue(Q, T);
    while (!IsEmpty(Q)){ // 判断队列是否为空
        DeQueue(Q, p); // 将队列队头元素出队
        visit(p); // 访问p元素
        if (p->lchild != NULL) EnQueue(Q, p->lchild); // 如果其包含左孩子，左孩子入队
        if (p->rchild != NULL) EnQueue(Q, p->rchild); // 如果其包含右孩子，右孩子入队
    }
}

下一节内容是25、二叉树——构建二叉树…….

一定要把本节内容看懂再往下看，不然会非常痛苦的哦o(╥﹏╥)oo(╥﹏╥)oo(╥﹏╥)o

25、数据结构——二叉树——通过遍历构建二叉树上一篇

23、数据结构——二叉树——存储结构下一篇