23、数据结构——二叉树——存储结构

一、顺序存储方式

结构体

1
2
3
4
5
#define MaxSize 100
struct TreeNode {
    ElemType data; // 结点中
    bool isEmpty; // 结点是否为空	
}t[MaxSize];

初始化所有结点均为空

1
2
3
4
// 注意，我们之后正式存储数据的时候习惯从t[1]开始存储，这样的好处是可以将下标和数据的编号一一对应上，如下图
for (int i = 0; i < MaxSize; i++) {
    t[i].isEmpty = true;
}
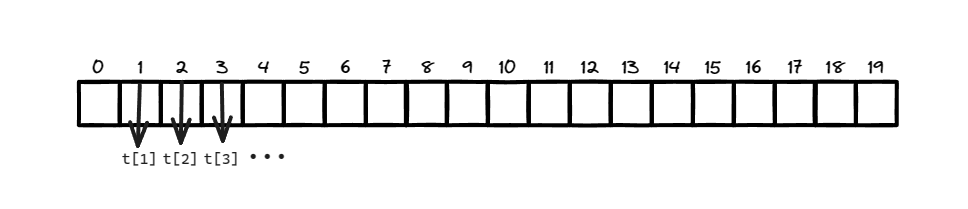
image-20240305164504577

完全二叉树中有n个结点，则

  • 判断 i 是否有左孩子？ 2i <= n

  • 判断 i 是否有右孩子？2i + 1 <= n

  • 判断 i 是否是叶子结点 / 分支结点？
    $$
    i > \lfloor \frac{n}{2}\rfloor
    $$

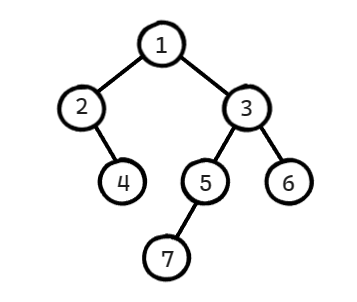
如果此时的二叉树是非完全二叉树，那么顺序存储就失效了（如图）

image-20240305165724571

​ 因此我们这里顺序存储的方式需要稍微变一下，变为下图这种形式：

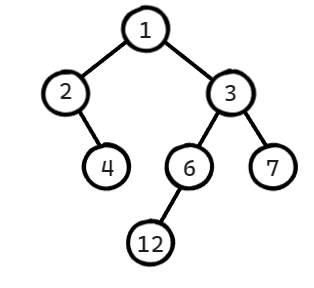
image-20240305165921550

​ 这时候我们如果还希望查找某个结点是否有左孩子、右孩子等，就必须通过结构体中的 isEmpty 来判断了。比如说你想查6结点是否有左孩子结点，此时你就可以通过判断t[2*i].isEmpty 来判断左孩子结点是否为空。

注意

​ 当然，虽然顺序存储查找元素的速度是很快，这里顺序存储的缺点也是非常明显的！比如说：他的空间利用率特别低！所以我们如果想使用顺序存储方式存树，一般只建议存完全二叉树。

二、链式存储结构

结构体

1
2
3
4
5
6
7
8
9
// 这里可以自行随便设置多个元素，表示一个结点中的所有数据
struct ElemType{
    int value;
};

typedef struct BiTNode {
    ElemType data;
    struct BiNode *lchild, rchild;
}BitNode,*BitTree;

提问

  • 对于n个==二叉链表==共有多少个==空链域==？除了根节点外，其他n-1个结点的头上都会连接1个结点，对不对？我们又知道一共是有2*n个指针域的，那么空指针域不就等于2n - (n - 1) = n + 1个了吗？答案就是n + 1。（可结合下图进行理解）

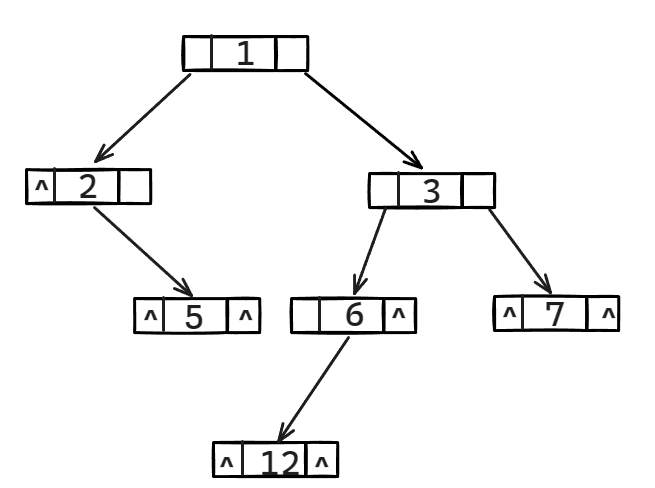
    image-20240305173202168

定义一棵空树

1
BitTree root = NULL;

插入根节点

1
2
3
4
root = (BitTree) malloc(sizeof (BitTree));
root -> data = {1};
root -> lchild = NULL;
root -> rchild = NULL;

插入新节点

1
2
3
4
5
6
BitTree * p = (BitTree *)malloc(sizeof (BitTree));
p -> data = {2};
p -> lchild = NULL;
p -> rchild = NULL;
root -> lchild = p; // 作为根节点的左孩子
// 请看下图进行理解
image-20240305172945350

下面介绍一下问题：如何查询1个结点是否有孩子结点（编号是从1开始的），这个问题就需要等到下一节的遍历的时候来讲了

下一节内容是24、二叉树——前中后序遍历…….

​