22、数据结构——二叉树——定义+性质
定义
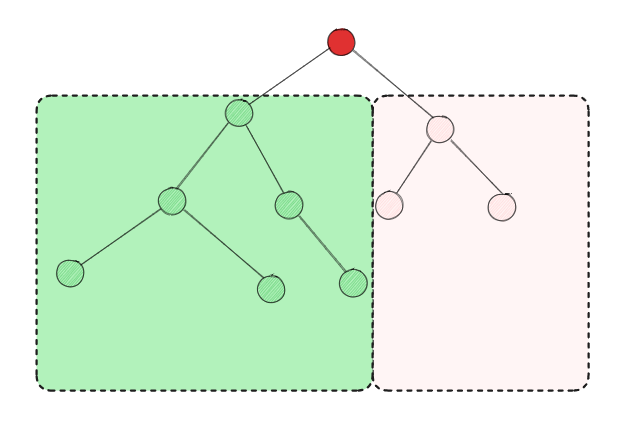
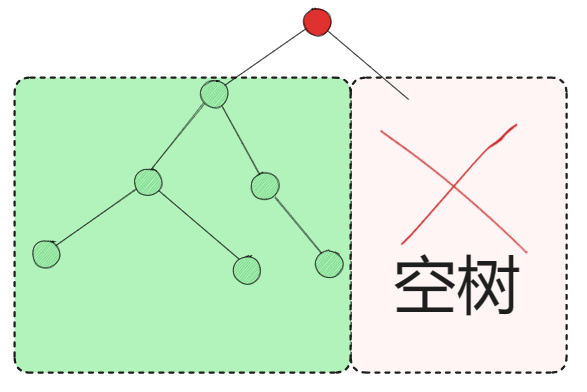
是n(n>=0)个结点的有限集合。空二叉树,即n=0。
或者由一个根节点和两个互不相交的被称为根的左子树和右子树组成。左子树和右子树又分别是一棵二叉树。
特点:
- 每个结点最多只有两个子树
- 左右子树不可以颠倒(二叉树是有序树,因此它和度为2的有序树是有区别的)
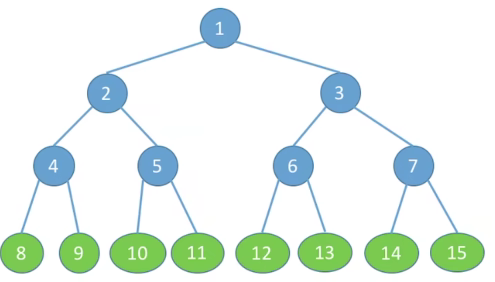
满二叉树
$$
一棵高度为h,且含有2^h - 1个结点的二叉树,不能多也不能少
$$
特点
- 只有最后一层有叶子结点
- 不存在度为1的结点
- 按层序从1开始编号,结点i的左孩子为2i,右孩子为2i+1,结点i的父节点为i/2进行上去取整 (如果有的话)
完全二叉树
当且仅当每个结点都与高度为h的满二叉树中编号为1~n结点一一对应。
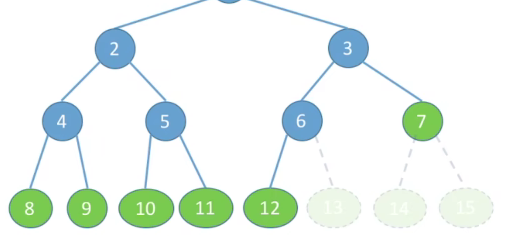
特点
- 只有最后两层可能有叶子结点
- 最多只有一个度为1的结点
- 按层序从1开始编号,结点i的左孩子为2i,右孩子为2i+1,结点i的父节点为i/2进行上去取整 (如果有的话)
注意: 如果大家对于这里的一一对应没有看太明白,就看下面的这个例子,这个不属于完全二叉树。
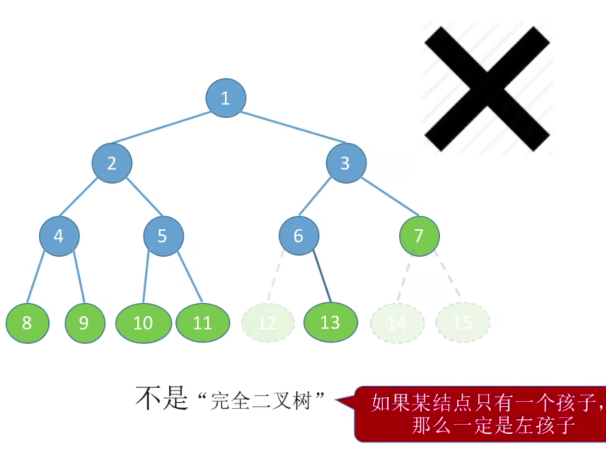
二叉排序树(用于元素的排序和搜索)
一棵二叉树或者是空二叉树,或者是具有如下性质的二叉树:
- 左子树上的所有结点的关键字均小于根结点的关键字
- 右子树上的所有结点的关键字均大于根结点的关键字
- 左子树和右子树又各是一棵二叉排序树
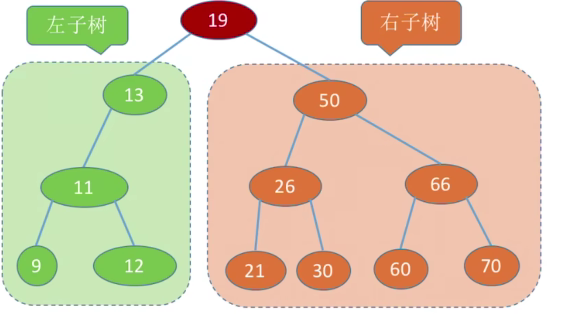
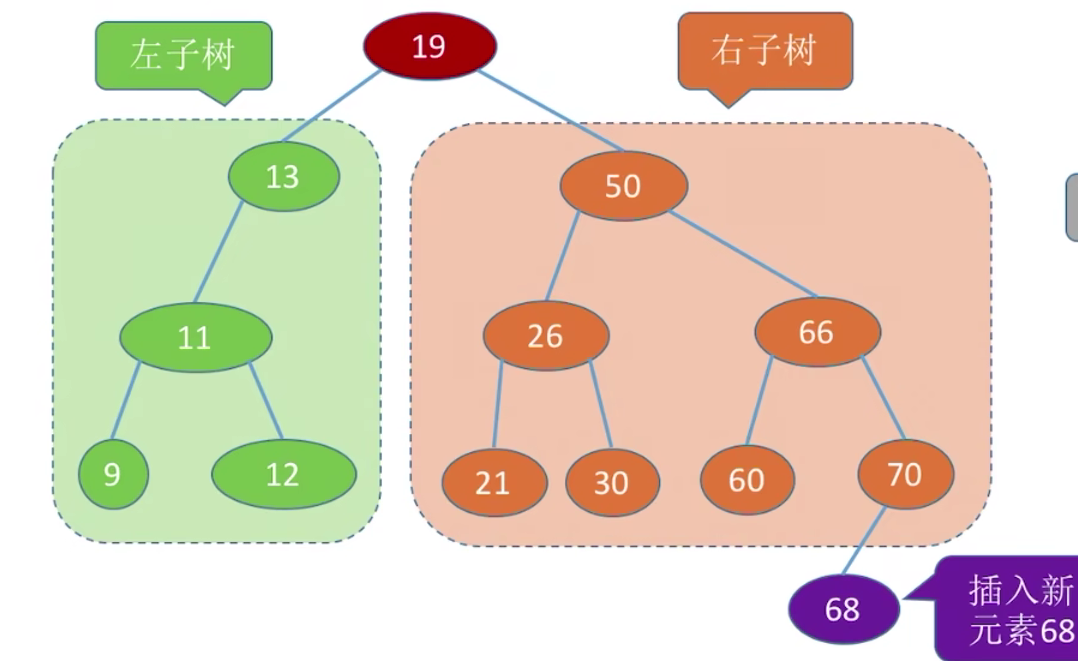
如果按照这种规则,比如我们想将68加入这个数里面去,我们一般就是这样的,首先从19开始和68进行大小比较,68大,进入右子树中,现在来到节点50,和68比较,68大,进入右子树,继续是66和68比较,68大,进入右节点,和70进行比较,68小,同时发现节点70没有左节点,所以直接插入即可。等到我们学习到后阶段,这种类型的代码肯定是要随手可写的,现在大家需要做到的主要就是可以把我上面介绍的思路理清楚即可。现在随意给出一个数组[4,5,1,2,3],大家可以尝试着将这个数组构造成下面的树。后面有答案。
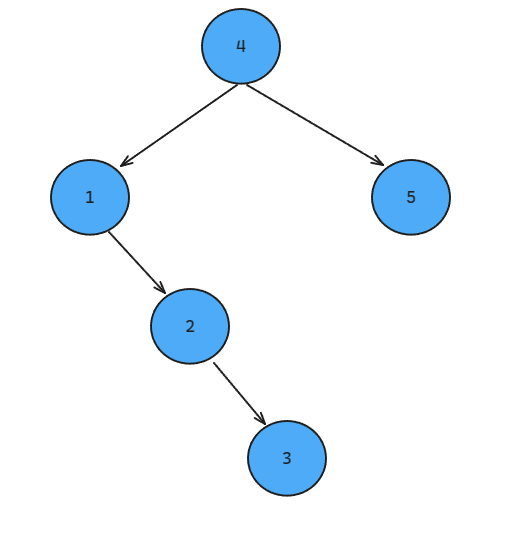
平衡二叉树(相比于一般的二叉排序树而言搜索效率更高)
树上任一结点的左子树和右子树的深度之差不超过1
例子:左边的是平衡二叉树,右边的不是。但是二者都是二叉排序树,大家观察一下这两个图搜索某一个数的时候你会发现,第1个图的效率明显会比第2个图快得多,比如:你要搜索66,第1个图首先比较50和66的大小,50<66,进入右子树,然后发现6666,1步就找到了。如果是第2个图来搜,首先26和66比较,22<66,进入子树,30和66比较,30<66,进入右子树,….,最后找到66

详细构造方法后续还会详细介绍!
二叉树的一些常用性质
设非空二叉树中度为0、1和2的结点个数分别为n
0、n1和n2,则==n0=n2+ 1==证明:
- n = n
0+ n1+ n2 - n = n
1+ 2n2+ 1**(因为树的结点个数=总度数 + 1)** - 因此有: n
0= n2+ 1->n0+ n2一定是奇数
- n = n
二叉树第 i 层最多2^i-1^ 个结点(i>=1)
高度h的二叉树最多2^h^ - 1个结点(满二叉树)
完全二叉树的一些常用性质
具有n个(n>0)结点的==完全二叉树的高度h为:==
$$
\lceil log_2(n+1)\rceil 或者 \lfloor log_2n \rfloor + 1\
2^{h - 1} - 1 < n \le 2^{h}-1\
……\
2^{h-1}\le n <2^{h}
$$完全二叉树最多一个度为1的结点,即n
1=0或1如果完全二叉树有2k个结点,必有==n
1=1,n0=k,n2=k-1==如果完全二叉树有2k - 1个结点,必有==n
1=0,n0=k,n2=k-1==