25、数据结构——二叉树——通过遍历构建二叉树
前言
这部分可以说是无论是考研还是期末考试都是非常喜欢出这种类型的题目的,只不过考研的话可能会更加恶心,没有考研需求的同学把这里看懂,复习的时候会轻松很多!
注意
如果我们现在不知道一棵树长什么样子,只知道这棵树的前中后序、层次遍历的一种,我们是不可以确定一棵二叉树的。
如果我们需要确定一颗二叉树,就至少需要前序/后序/层次遍历 + 中序遍历。
前序+中序遍历序列
前序遍历序列: 根节点 左子树前序遍历序列 右子树前序遍历序列
中序遍历序列: 左子树前序遍历序列 根节点 右子树前序遍历序列
那么前序遍历序列的第一个结点不就是根节点吗?,然后我们就可以根据中序遍历序列找到根节点从而确认左右子树有哪些构成了对不对?下面我们需要做的就是反复执行这么上述操作,现在我这么讲肯定是非常抽象的,下面我们通过例子来理解:
前序遍历序列:A D B C E
中序遍历序列:B D C A E
第一步:找到根节点A,再在中序遍历确定左右子树,如图
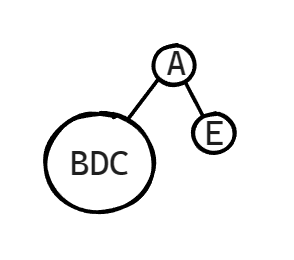
第二步:然后我继续分析左右子树,左子树的话我们就可以通过前序遍历序列继续确认其根节点,然后就是前序遍历确认左右子树,如DBC对应着D就是根节点,再在中序遍历找D,左子树为B,右子树就为C,如图
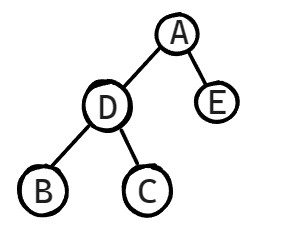
现在给一个例子大家自己尝试一下,下面有答案:
前序遍历:D A E F B C H G I
中序遍历:E A F D H C B G I










第一步
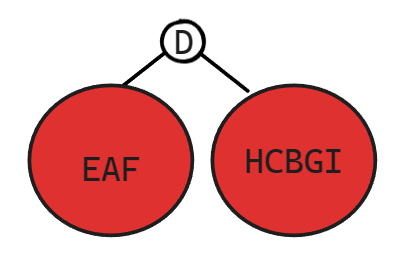
第二步
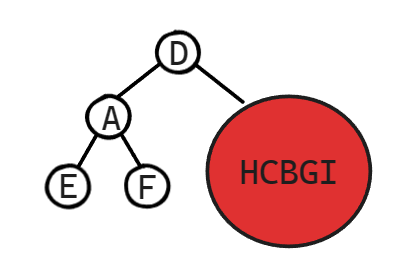
第三步
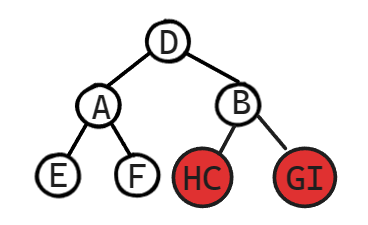
第四步
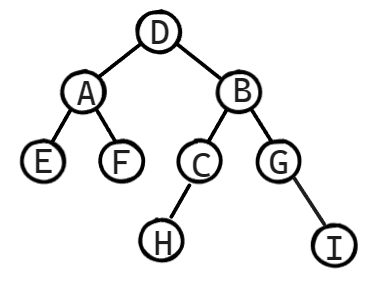
注意:为了保险起见,大家可以在这里对自己画的树进行验证一下,自己按照前序遍历和中序遍历读一次看看对不对
后序+中序遍历序列(和前面的寻找方法几乎一模一样,只不过我们前序遍历确认根节点是通过看第1个结点,后序遍历则是看最后1个结点确认根节点的)
后序遍历序列: E F A H C I G B D
中序遍历序列: E A F D H C B G I
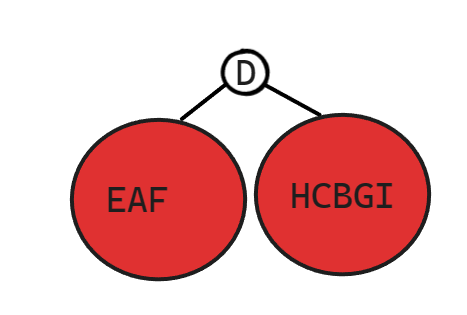
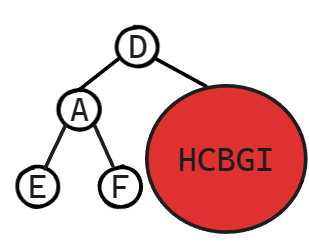
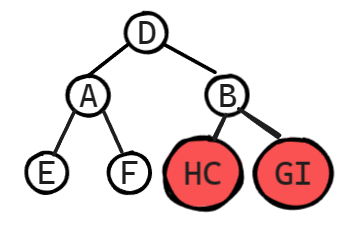
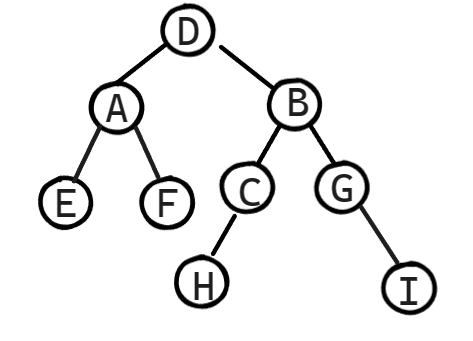
持续更新……