前言
对于普通二叉树而言,现在提出一个问题,如果随意给出你一个结点p,现在需要你找到它中序遍历对于结点p而言在遍历的时候的前驱或者后继(注意:这个的前驱是指中序遍历的时候的前驱哟!) 。这个时候就会比较麻烦了,你必须对这课树从根节点出发重新进行一次中序遍历,同时还需要准备两个指针分别指向当前结点p和当前结点的前驱pre两个。但是这样的话就会非常不方便,效率也会很低,因此我们就引入了线索二叉树来解决这种特殊情况问题。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
typedef struct BiTNode {
ElemType data;
struct BiNode *lchild, rchild;
}BitNode,*BitTree;
BitNode *p;
BitNode *pre = NULL;
BitNode *final = NULL;
void visit(BitNode *q) {
if (q==p) {
final = pre;
} else {
pre = p;
}
}
void InOrder(BitTree T){
if (T!=NULL){
InOrder(T->lchild);
visit(T);
InOrder(T->rchild);
}
}
|
注意:如果你是以考研为目标,我下面的内容写得比较简单,可能不是非常好懂,这里开始就必须大家自己去寻找一些视频进行观看了,反之如果不是以考研为目标,这一节内容简单了解即可,可以先行跳过,期末有需求再额外学习
一、中序线索二叉树
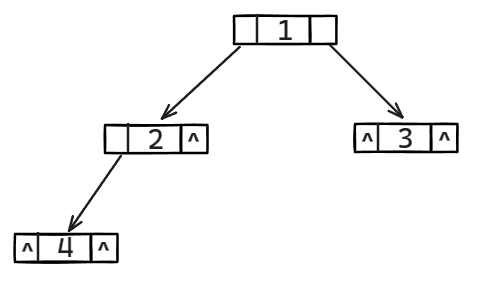
对于一个 n 个结点的二叉树,有 n + 1 空指针域!可用来记录前驱和后继信息。
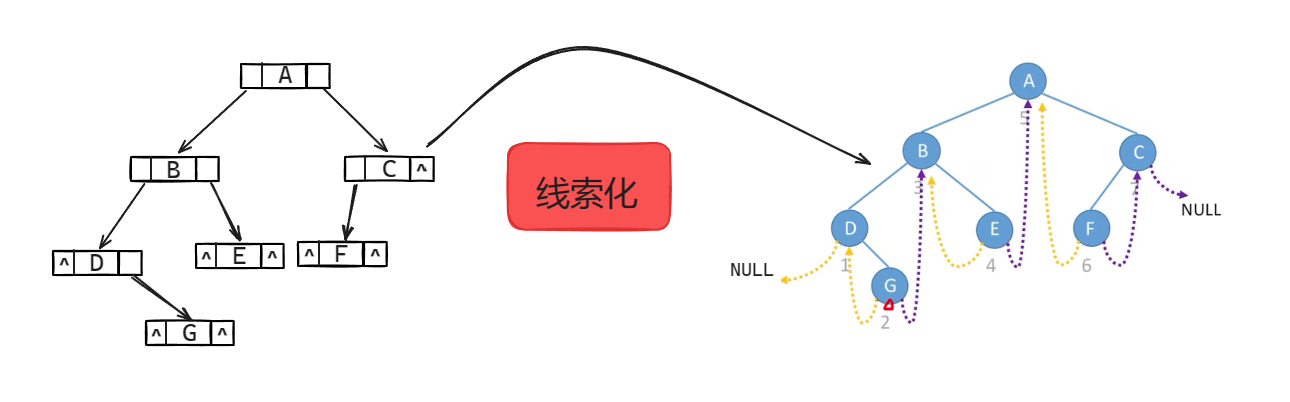
前驱线索: 左孩子指针充当
后驱线索: 右孩子指针充当
存储结构

1
2
3
4
5
6
7
8
9
|
typedef struct ThreadNode{
ElemType data;
struct ThreadNode *lchild, *rchild;
int ltag,rtag;
}ThreadNode,*ThreadTree;
ThreadNode *pre = NULL;
|
中序线索二叉树的构建
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| void visit(ThreadNode *q) {
if (q -> lchild==NULL) {
q -> lchild = pre;
q -> ltag = 1;
}
if (pre != NULL && pre -> rchild == NULL){
pre -> rchild = q;
pre -> rtag = 1;
}
pre = q;
}
void InThread(ThreadTree T) {
if (T!=NULL){
InThread(T->lchild);
visit(T);
InThread(T->rchild);
}
}
void CreateInThread(ThreadTree T){
pre = NULL;
if (T != NULL) {
InThread(T);
if (pre -> rchild == NULL) {
pre -> rtag = 1;
}
}
}
|
二、先序线索二叉树(和中序的差不多)
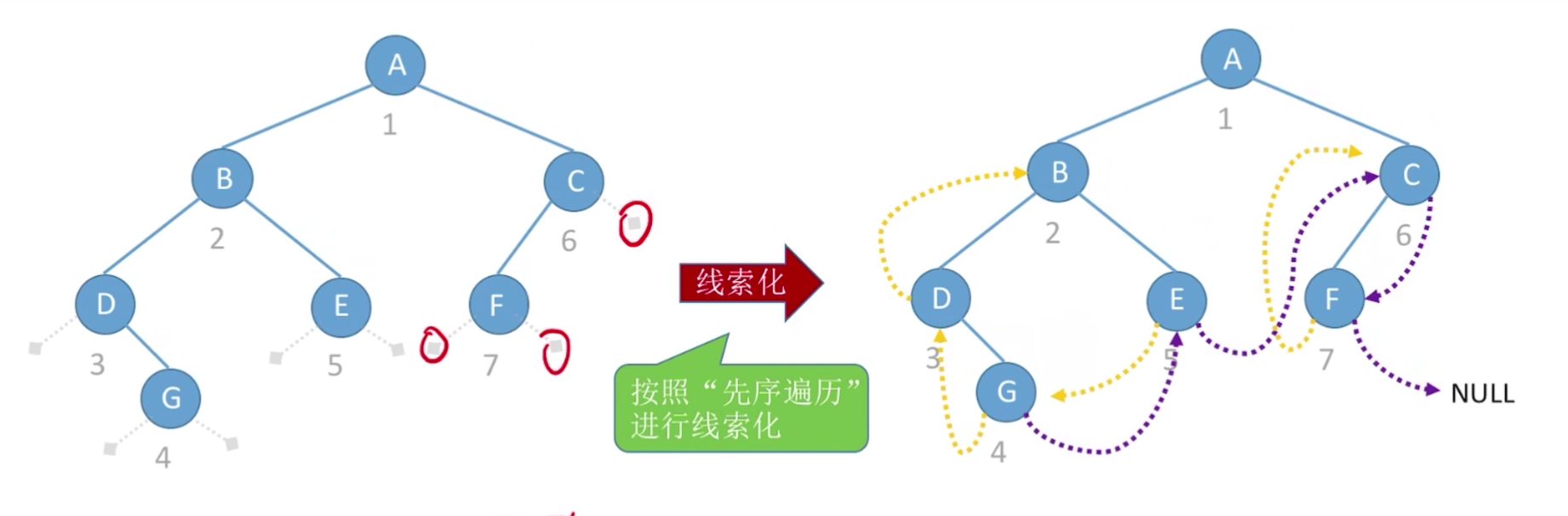
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| void visit(ThreadNode *q) {
if (q -> lchild==NULL) {
q -> lchild = pre;
q -> ltag = 1;
}
if (pre != NULL && pre -> rchild == NULL){
pre -> rchild = q;
pre -> rtag = 1;
}
pre = q;
}
void PreThread(ThreadTree T) {
if (T!=NULL){
visit(T);
if (T->ltag == 0) PreThread(T->lchild);
PreThread(T->rchild);
}
}
void CreateInThread(ThreadTree T){
pre = NULL;
if (T != NULL) {
PreThread(T);
if (pre -> rchild == NULL) {
pre -> rtag = 1;
}
}
}
|
三、后序线索二叉树
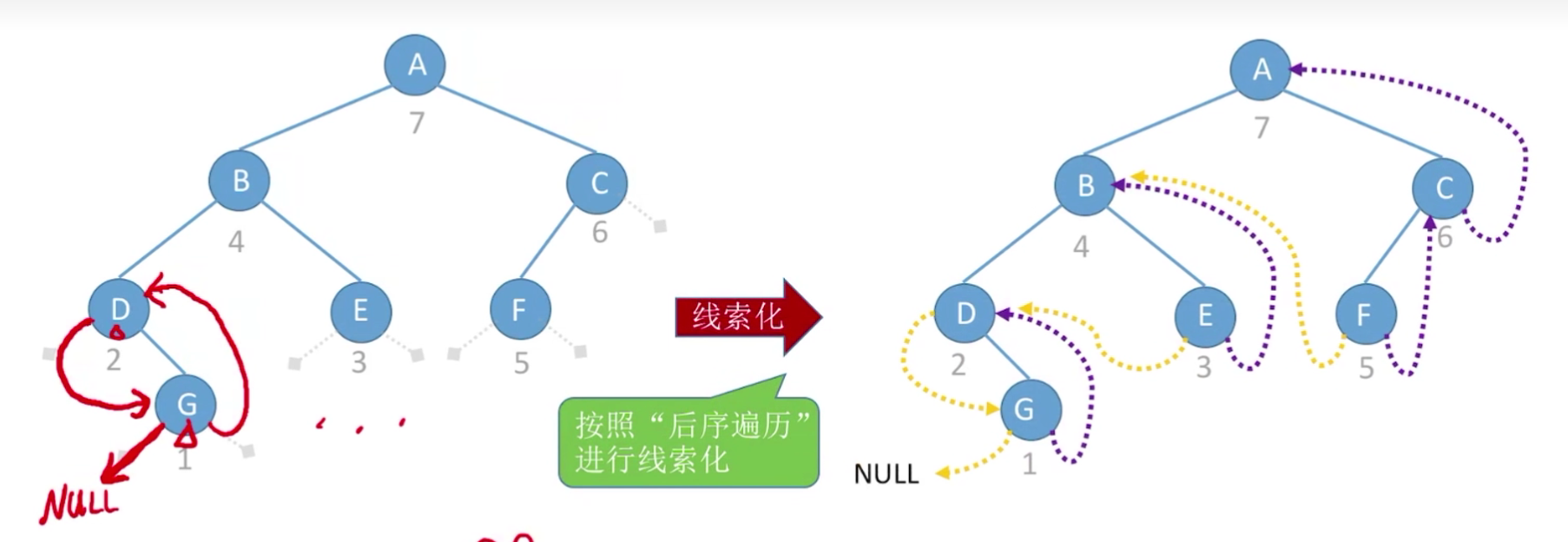
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| void visit(ThreadNode *q) {
if (q -> lchild==NULL) {
q -> lchild = pre;
q -> ltag = 1;
}
if (pre != NULL && pre -> rchild == NULL){
pre -> rchild = q;
pre -> rtag = 1;
}
pre = q;
}
void PostThread(ThreadTree T) {
if (T!=NULL){
PostThread(T->lchild);
PreThread(T->rchild);
visit(T);
}
}
void CreateInThread(ThreadTree T){
pre = NULL;
if (T != NULL) {
PostThread(T);
if (pre -> rchild == NULL) {
pre -> rtag = 1;
}
}
}
|
一节内容是27、树——存储结构…….
一定要把本节内容看懂再往下看,不然会非常痛苦的哦o(╥﹏╥)oo(╥﹏╥)oo(╥﹏╥)o




