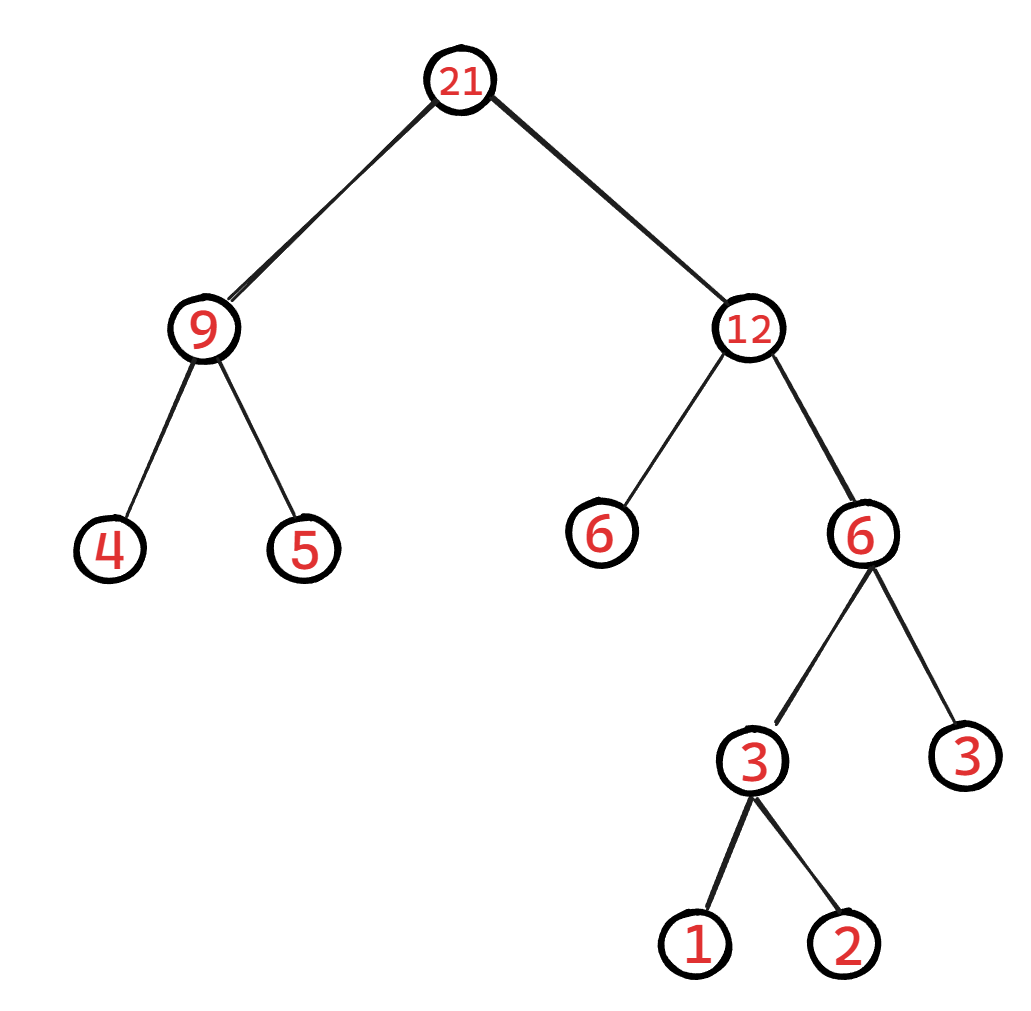
29、数据结构——树——哈夫曼树和哈夫曼编码
带权路径长度
结点的权
有某种特殊含义的数值（表示节点的重要性等）
结点的带权路径长度
从树的根到该结点的路径长度（经过的边数） 与节点上的数的乘积
树的带权路劲长度
所有的叶子结点的带权路径长度之和（WPL）
$$
WPL=\sum^{n}_{i=1}w_il_i
$$
下面就来举两个例子来介绍一下怎么计算（考的概率蛮大）
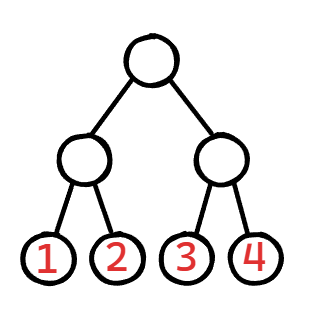$$
WPL=1 \times 2 + 2 \times 2+3 \times2+4\times2=20
$$
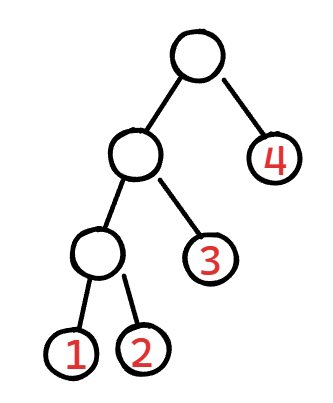$$
WPL=1\times3+2\times3+3\times2+4\times1=10
$$
对于n个带权结点的二叉树中，其中WPL最小的二叉树称为哈夫曼树，也称为最优二叉树。那么我们应该如何通过已知节点来构造出一棵WPL最小的二叉树呢，这就是我们今天要学的一个重点内容，请看下一个内容。
哈夫曼树的构造
$$
\begin{flalign}
&给定n个权值分别为w_1w_2,w_n的结点，构造哈夫曼树的算法描述如下：\
&1)将这n个结点分别作为n棵仅含一个结点的二叉树，构成森林F。\
&2)构造一个新结点，从F中选取两棵根结点权值最小的树作为新结点的左、右子树，\
&并且将新结点的权值置为左、右子树上根结点的权值之和。\
&3)从F中删除刚才选出的两棵树，同时将新得到的树加入F中。\
&4)重复步骤(2)和(3)，直至F中只剩下一棵树为止。&
\end{flalign}
$$
这是一个官方化的构造方式，下面我们就来一个例子来讲一下如何构造哈夫曼树：
现在给出几个节点，需要你构造出一个哈夫曼树：
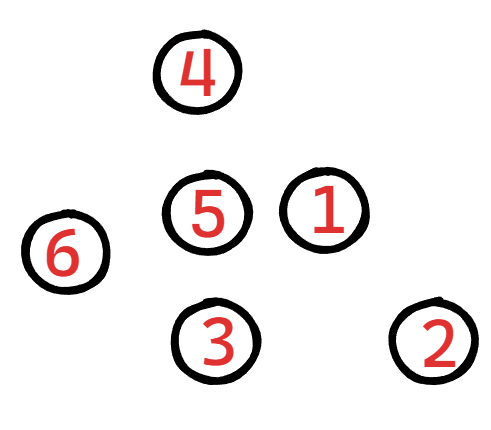
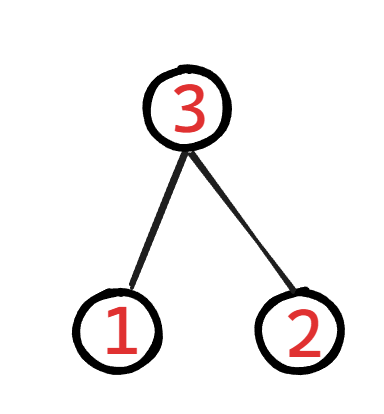
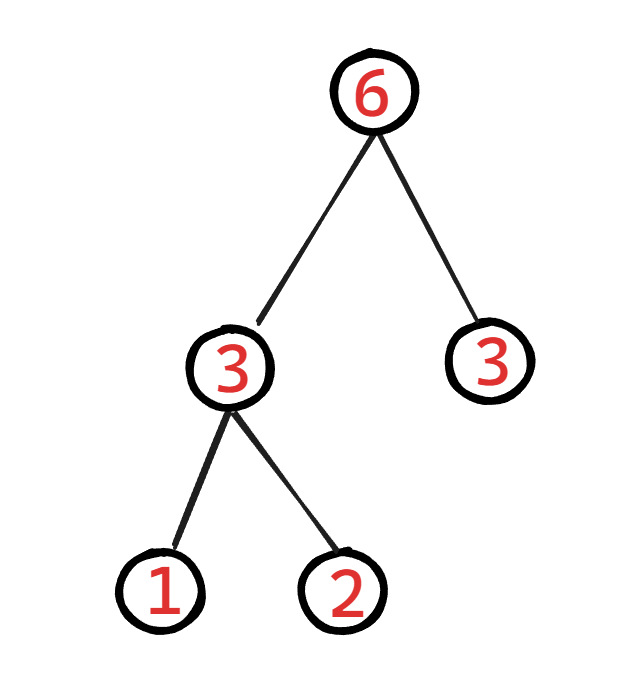
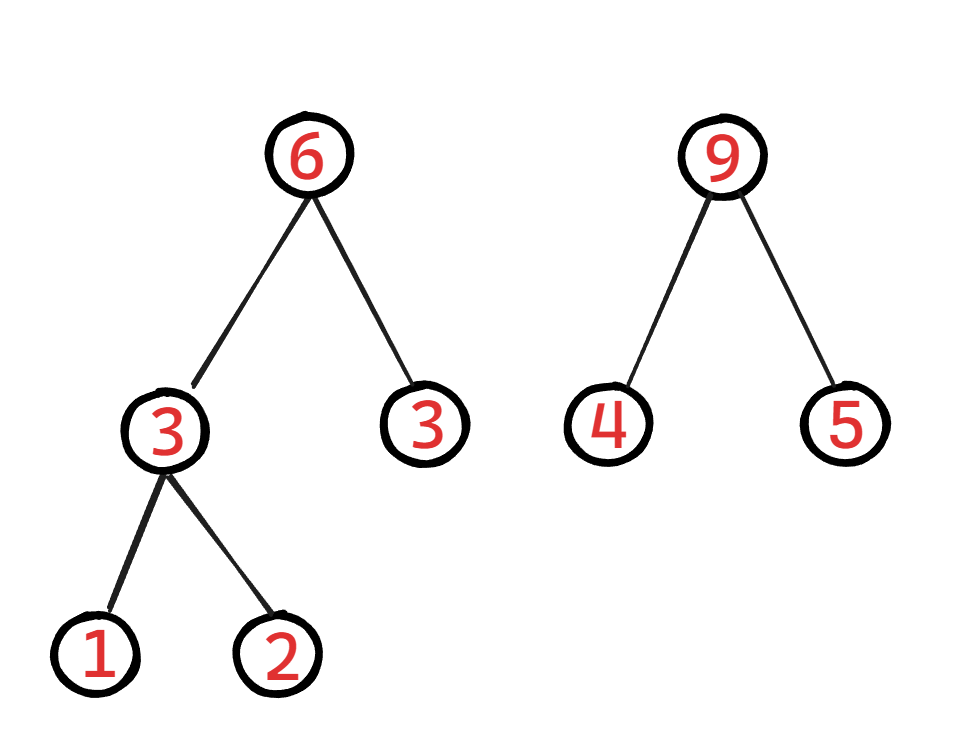
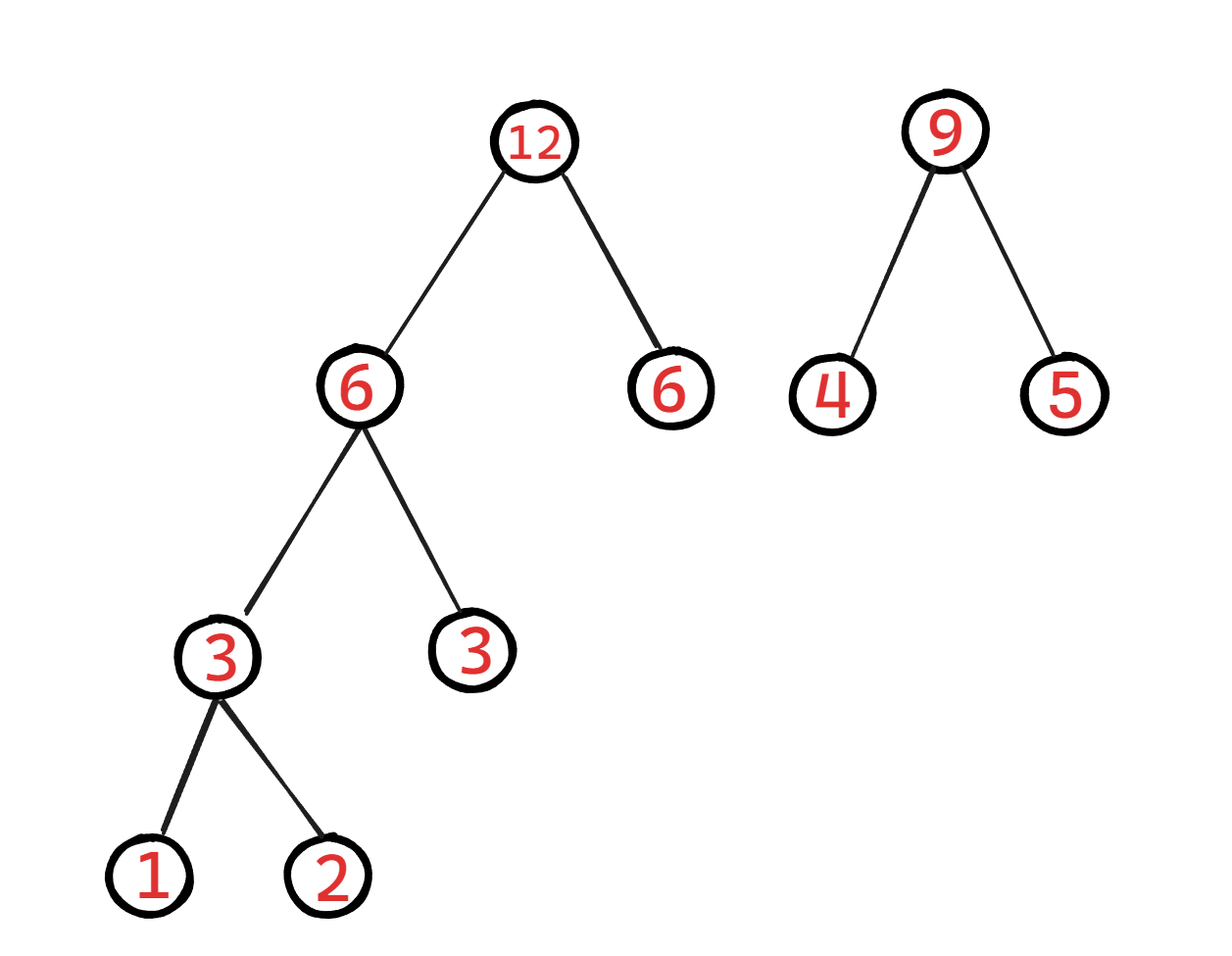
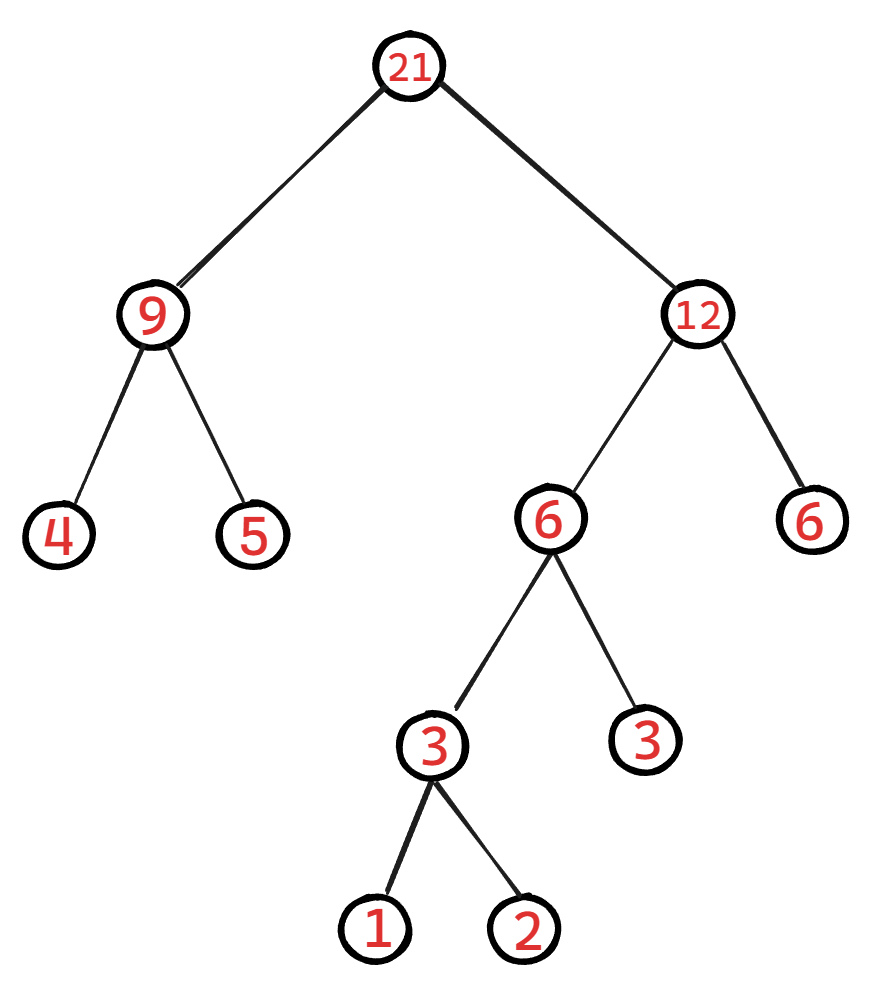
注意：哈夫曼树不是唯一的，但是它们的WPL一定是相同的，比如我再写另一个哈夫曼树
