27、数据结构——树——存储结构

森林的基本概念

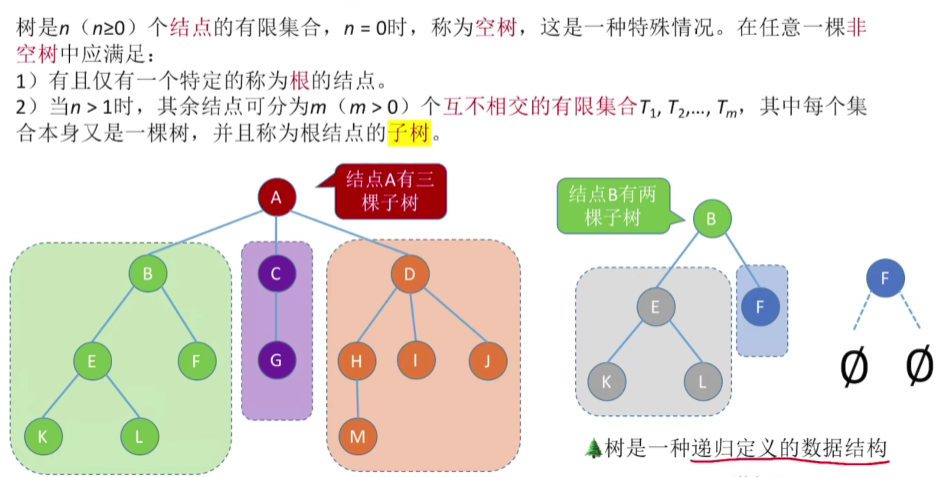
image-20240310132742766

一、双亲表示法（顺序存储）

描述

每个结点中保存指向双亲的“指针”

结构体

1
2
3
4
5
6
7
8
9
10
#define MAX_TREE_SIZE 100 		 // 树中最多的结点数
typedef struct { 		         // 树的结点定义
    ElemType data;        		 // 数据元素
    int parent;           		 // 双亲位置域，当parent==-1的时候该结点无双亲结点，也就是根节点
}PTNode;

typedef struct {
    PTNode nodes[MAX_TREE_SIZE]; // 双亲表示 
    int n;                       // 结点数
}PTree;
注意：这里大家如果对于后面代码大概有个怎么写的概念的话，那么就可以证明树这节内容你掌握得还算要得，如果对于后面我需要如何实现代码一点思路都没有，那么你就最好还是先把前面的内容再温习温习再回到这里继续观看下面的内容。

优点

​ 查找某个特定结点的双亲结点时候会很方便

添加节点和删除节点

添加叶子节点： 加上节点的时候需要将其双亲节点记录一下。

删除叶子节点： 删除节点的时候需要将其双亲节点删除：

  • 这个时候你可以选择将该结点的双亲结点设置为-1，表示该位置是空的；（缺点：在再次进行遍历操作的时候会出现空数据情况从而导致遍历变慢，同时还会存在空间利用率低的情况）
  • 也可以将我们存储数组的最后一个元素移动到这个删除节点的位置以保证所有的存储单元对应结点都是有效的

删除分支结点： 这个时候我们需要删除的就是以这个分支节点为根节点的子树中所有的结点了。

二、孩子表示法（顺序+链式存储）

描述

​ 顺序存储各个节点，每个结点中保存孩子结点的链表头指针。

结构体

1
2
3
4
5
6
7
8
9
10
11
12
struct CTNode {
    int child; // 孩子结点在数组中的位置
    struct CTNode *next; // 下一个孩子
};
typedef struct  {
    ElemType data;
    struct CTNode *firstChild; // 第一个孩子
} CTBox;
typedef struct {
    CTBox nodes[MAX_TREE_SIZE];
    int n, r; // 结点和根的位置
}CTree;

图解

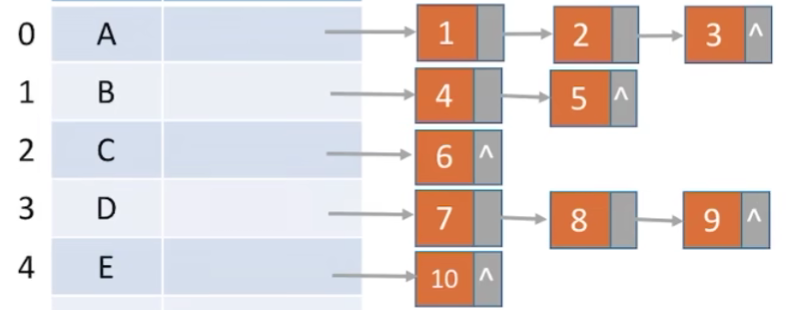
image-20240310141218213

优点和缺点

  • 这种存储方式，很明显：寻找某个结点的孩子结点就会变得非常方便，但是找双亲结点就有点麻烦了（找双亲这里提供一种方法，就是对所有结点A/B/C/D/E的孩子结点进行遍历，由于一个结点只有一个双亲结点，所有一旦搜索到寻找结点为X结点的孩子结点，那么X结点就是寻找结点的双亲结点）

三、孩子兄弟表示法（链式存储）

结构体

1
2
3
4
typedef struct CSNode {
    ElemType data; // 数据域
    struct CSNode *firstchild, *nextsibling; // 第一个孩子结点和兄弟结点
}CSNode,*CSTree;
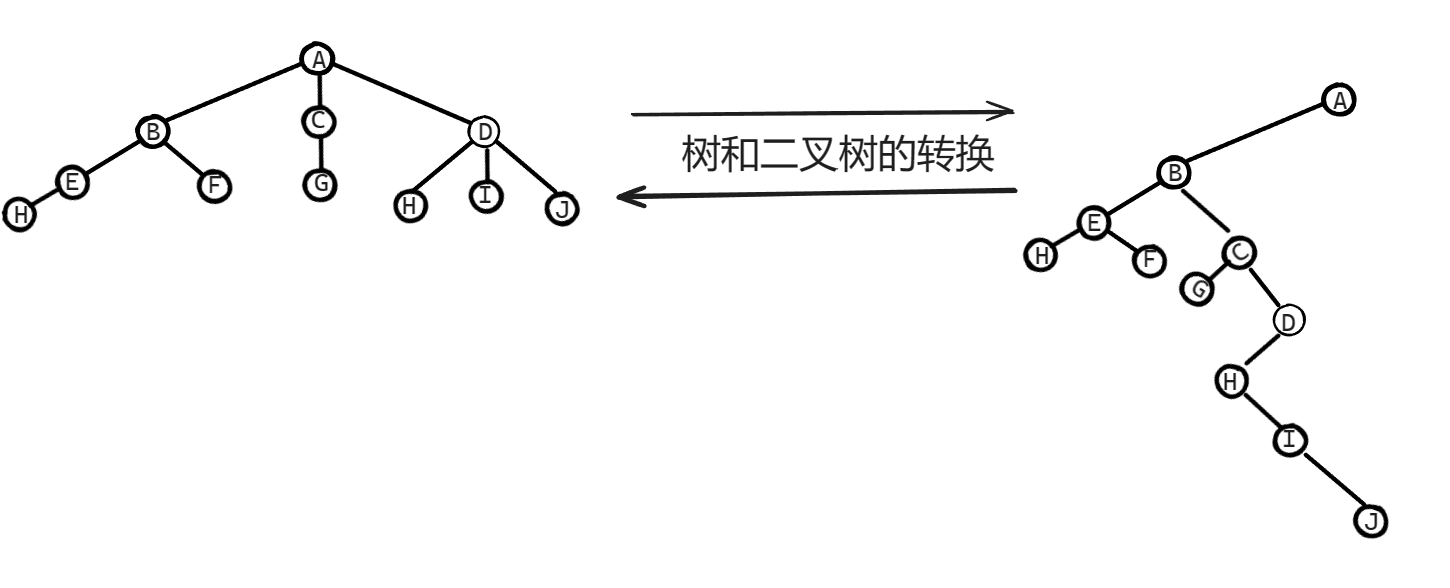
image-20240310143814680

我们之后还会学习如何进行树和二叉树和森林之间的转换，这里介绍的就是树转换为二叉树。

详细过程请看 链接 7min25s~末尾 这一部分是期末考试的重大考点之一

一节内容是28、树——树和森林的遍历…….

一定要把本节内容看懂再往下看，不然会非常痛苦的哦o(╥﹏╥)oo(╥﹏╥)oo(╥﹏╥)o