21、数据结构——树——定义+性质
基本概念
树是n个结点的有限集合,n=0,为空树,这是一种特殊情况。
树就由一个一个结点和连线组成的,具体性质术语见下。
专业术语
空树: 结点数为0的树
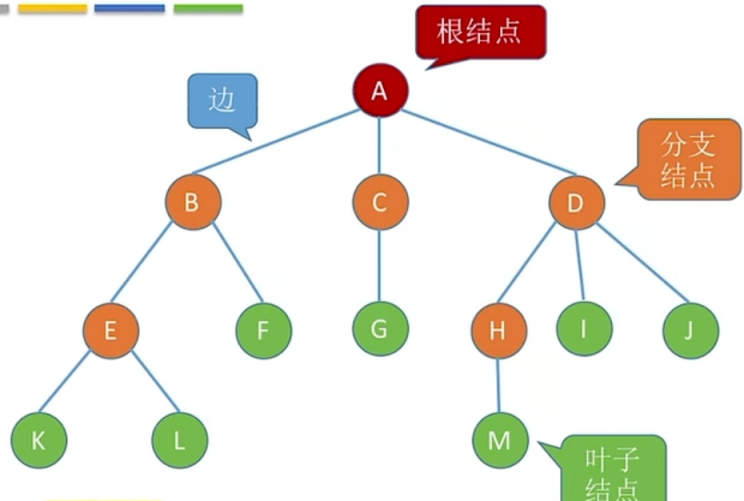
叶子结点:没有后继的结点的结点
分支结点: 有后继的结点
非空树
- 有且仅有1个根节点
- 除了根节点外,任何一个结点有且仅有一个前驱
- 每个结点可以有0个或者多个后继结点
子树(看例子理解)
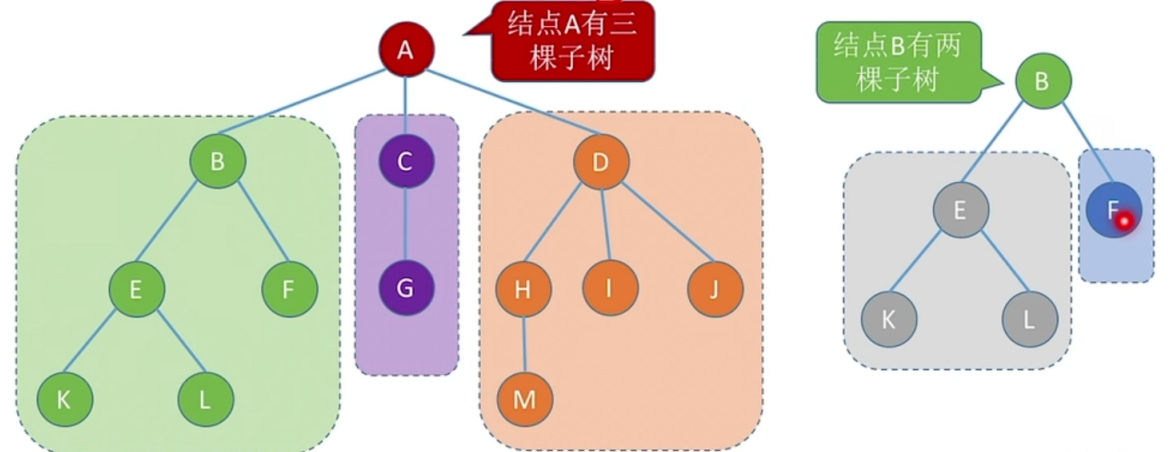
树是一种递归定义的数据结构
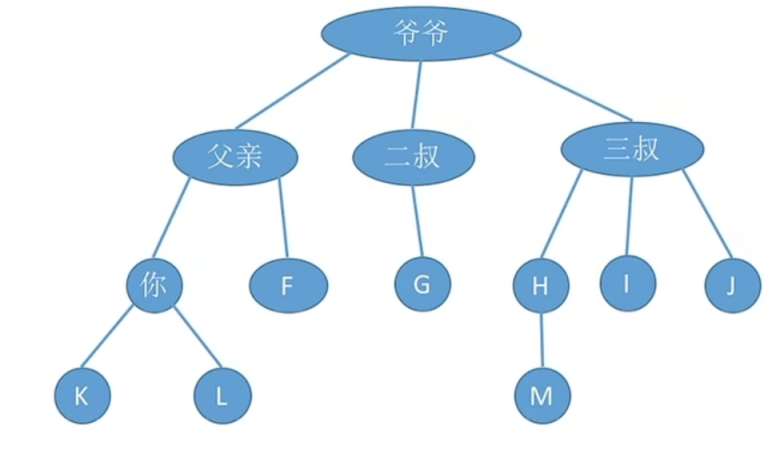
祖先结点: 爷爷是所有结点的祖先结点。
子孙结点: 某一个结点子树的所有结点,比如说:爷爷结点下面所有的结点都是爷爷结点的子孙结点;你、F、K、L是父亲的子孙结点。
双亲结点(父结点): 你的父结点为父亲,父亲的父节点为爷爷
孩子结点: 你的孩子结点就是K、L。
兄弟结点: 具有同一个父结点的各结点彼此是兄弟结点。比如你的兄弟结点是F,但是G不是你的兄弟结点。
堂兄弟结点: 两个节点深度相同,但父节点不同,则它们是一对堂兄弟节点。比如:你和G是堂兄弟结点,不是兄弟节点。但是需要注意的是在有的教材上也把F看做你的兄弟结点,实际考题中遇到也不用担心,出现了堂兄弟结点的话题目的本意就只是让你知道这两个结点属于同一层。
两个结点之间的路径: 只能从上往下,就是那一条条连线,但是是有方向的需要注意。
路径长度: 经过几条边,比如爷爷->你需要经过2条路径。
结点的层次(深度): 从上往下数(默认是1开始), 比如说G结点的深度为3,M结点的深度为4
数的高度(深度): 总共多少层,下面树的高度为4
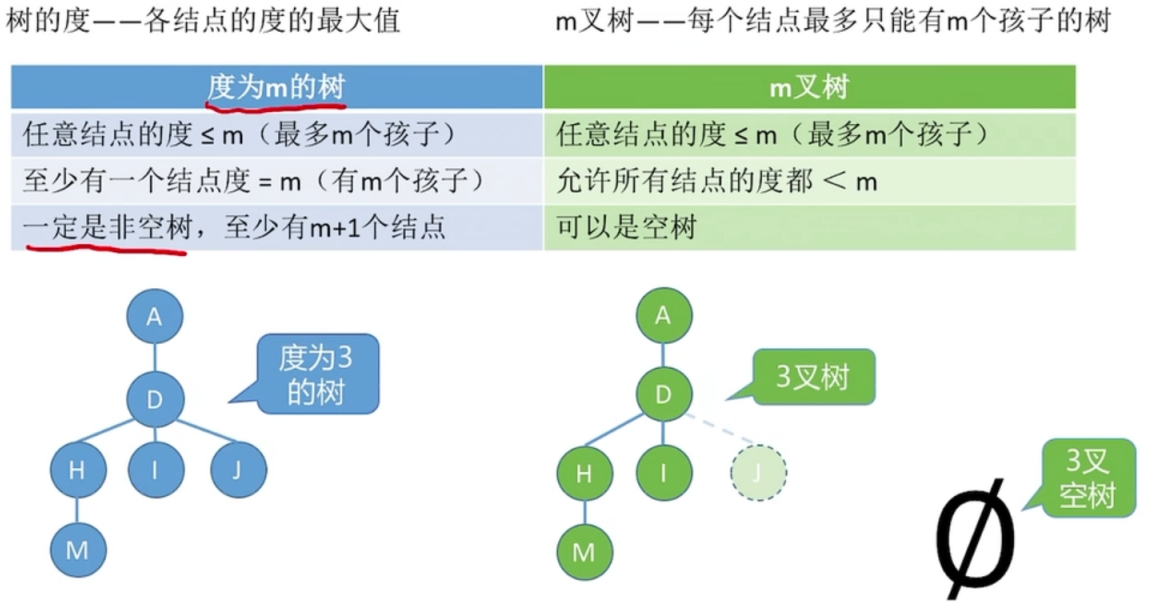
结点的度: 有多少个孩子结点(分支) ,叶子结点的度为0
树的度: 各结点的度的最大值,下面树的度为3
常见考点一:求结点数 结点数 = 总度数 + 1,这个可以设想一下,你将所有结点的度数加在一起就是每个结点的孩子结点,那么是不是我们只需要将这些孩子结点的数量加在一起之后再加上不包含在孩子结点里面的结点个数就可以算出所有的结点数量了,因此很明显下面的途中不包含在孩子结点中的就是爷爷结点,其他任意一个结点都是另一个结点的孩子结点。
常见考点二:度为m的树和、m叉数的区别
常见考点三:高度为h的m叉树最多有m^h^ - 1 / m - 1 个结点
注意:
- 第一层: m^0^ 个结点
- 第二层: m^1^ 个结点
- 第三层: m^2^ 个结点
- 第四层: m^3^ 个结点
- …..
- 最后你就是用等比数列的前n项公式即可
常见考点四:高度为h的m叉树至少有h个结点;高度为h、度为m的树至少h + m - 1个结点
- 高度为h的m叉树,你每层最少一个结点,因此h高度最少h层,最少也有h个节点
- 高度为h、度为m的树至少有一个结点的度为m,因此h - 1层的结点数为1,1层是m即可,最后结点数=h + m - 1
常见考点五:具有n个结点的m叉树的最小高度为
$$
\lceil log_m(n(m-1)+1)\rceil \
高度最小的情况–所有结点都有m个孩子\
证明:\
\frac{m^{h-1}-1}{m-1}\le n\le\frac{m^{h}-1}{m-1}\
m^{h-1}<n(m-1)+1\le mh\
h-1<log_{m}(n(m-1)+1)\le h\
h_{min}=\lceil log_{m}(n(m-1)+1)\rceil
$$
简单说一下什么是森林?
森林是m(m>0)棵互不相交的树的集合。
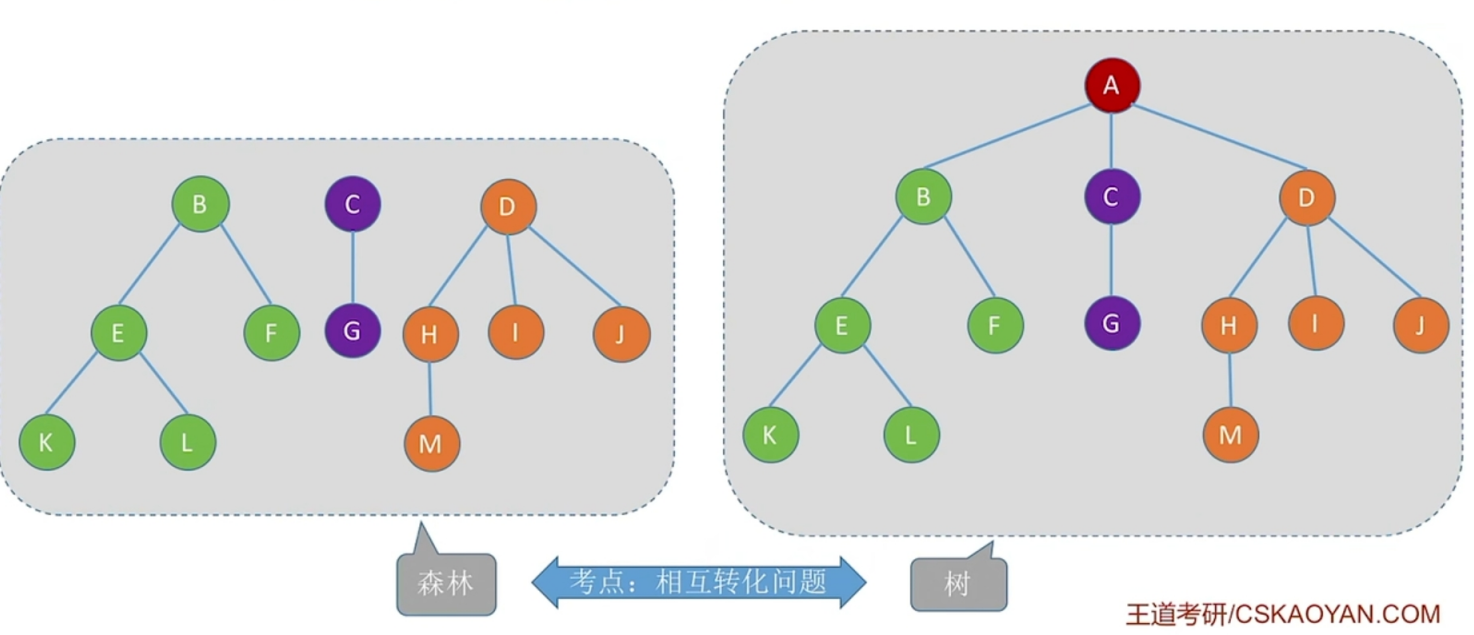
注意
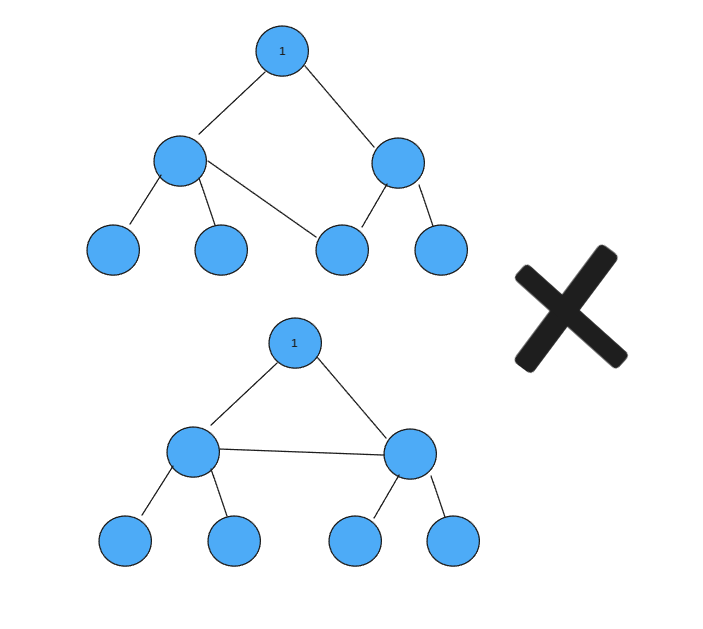
像下面这些类型的图就不属于树