28、数据结构——树——树和森林的遍历

一、树的遍历

1）树的先根遍历（和二叉树前序遍历是异曲同工的）

若树非空，先访问根节点，再依次对每棵树进行先根遍历

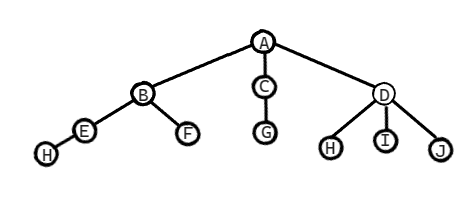
对于上面树的先根遍历序列应该为：A——>B——>E——>H——>F——>C——>G——>D——>H——>I——>J

// 树的先根遍历
void PreOrder(TreeNode *R){
    if (R!=NULL){
        visit(R);
        while (R有子树T){
            PreOrder(T); // 先根遍历子树
        }
    }
}

注意： 将树转换为二叉树，数的先根遍历序列与这课树相应的二叉树的先序遍历相同。下面的图就是上述图转换为的二叉树，前面已经说过转换方式，这里就不详细介绍了。

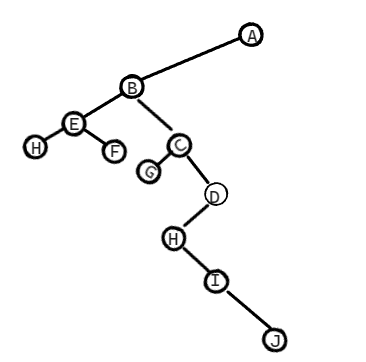
2）数的后根遍历（和二叉树后序遍历是异曲同工的）

若树非空，先依次对每颗子树进行后根遍历，最后访问根结点。

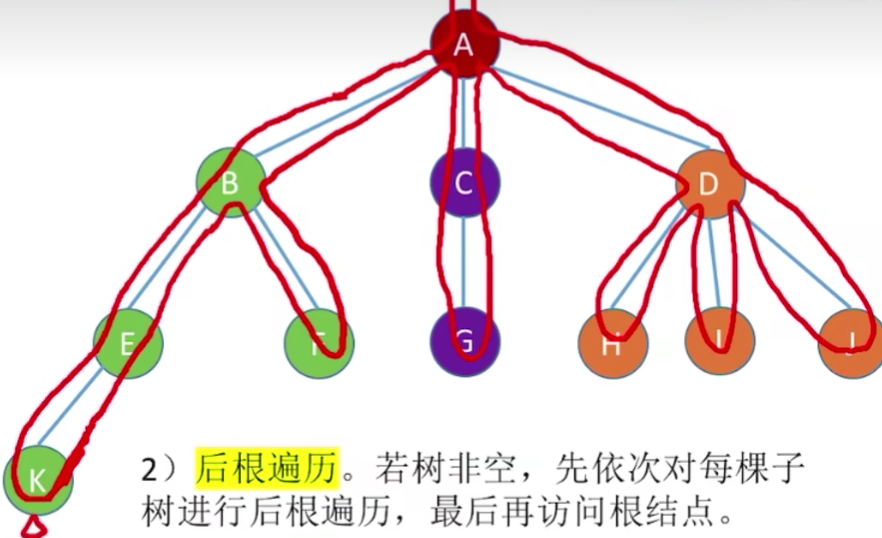
对于上面树的后根遍历序列应该为：H——>E——>F——>B——>G——>C——>H——>I——>J——>D——>A

// 树的后根遍历
void PostOrder(TreeNode *R){
    if (R!=NULL){
        while (R还有下一个子树T){
            PostOrder(T); // 后根遍历子树
        }
        visit(R); // 访问根结点
    }
}

注意： 将树转换为二叉树，数的后根遍历序列与这课树相应的二叉树的后序遍历相同。下面的图就是上述图转换为的二叉树，前面已经说过转换方式，这里就不详细介绍了。

3）层次遍历（这个应该就不需要那么详细介绍了吧，就是按照之前介绍过的方式遍历）

这棵树的层次遍历序列为：A——>B——>C——>D——>E——>F——>G——>H——>I——>J——>H

1	`// 這部分代码和之前的层次遍历都是同样的思路，如果大家忘记了就返回到24、数据结构——二叉树——前中后序、层次遍历去看看吧`

二、森林的遍历

森林定义

森林是m(m≥0)棵互不相交的树的集合。每棵树去掉根节点后，其各个子树又组成森林。

先序遍历

就是每棵树都进行一次先根遍历然后串在一起：

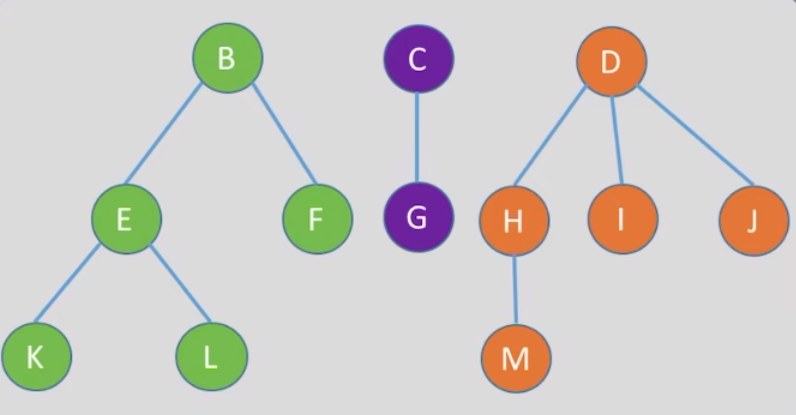
先根遍历为： B->E->K->L->F->C->G->D->H->M->I->J

注意： 森林的先序遍历序列和转换为的二叉树的先根遍历序列是相同的。

中序遍历（考得不多，但是必须了解一下！！！）

效果等效于依次对各个树进行后根遍历。

而转换成二叉树之后，二叉树的中序遍历就相当于森林的中序遍历

一节内容是29、树——哈夫曼树和哈夫曼编码…….

一定要把本节内容看懂再往下看，不然会非常痛苦的哦o(╥﹏╥)oo(╥﹏╥)oo(╥﹏╥)o

29、数据结构——树——哈夫曼树和哈夫曼编码上一篇

27、数据结构——树——存储结构下一篇