17、数据结构——特殊矩阵的压缩存储
一维数组的存储结构
就是最直白的存储方式,一个接着一个在内存中存储。
二维数组的存储结构
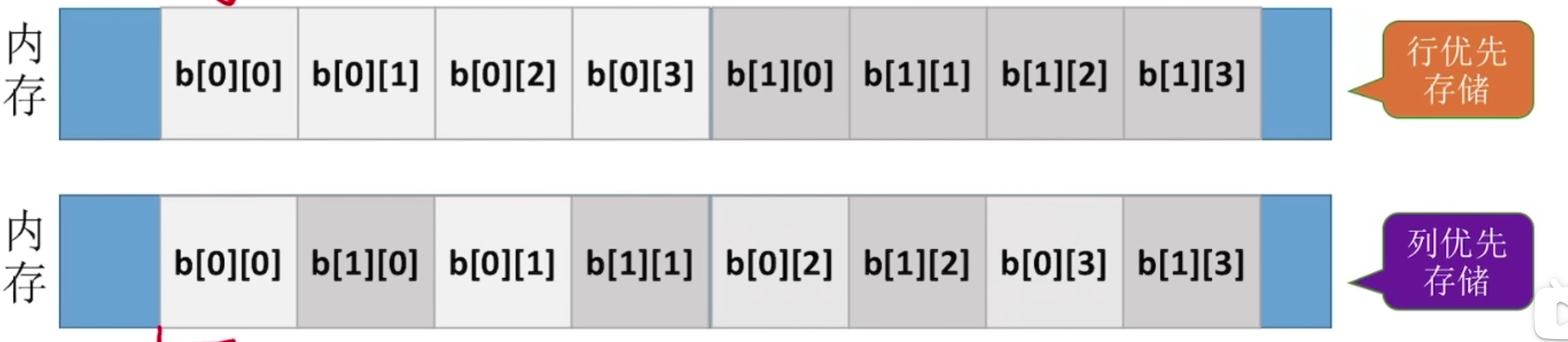
对于行优先存储:我们假设假设起始地址为LOC,那么对于数组b[N] [M]而言b[i] [j] 存储地址 = LOC + (i * N + j) * sizeof(ElemType)
对于列优先存储:我们假设假设起始地址为LOC,那么对于数组b[M] [N]而言b[i] [j] 存储地址 = LOC + (j * M + i) * sizeof(ElemType)
普通矩阵的存储

可以使用二维数组进行存储
注意:描述矩阵元素时,行、列号通常从1开始:而描述数组时通常下标从0开始**(具体看题目给的条件,注意审题!)**
对称矩阵的压缩存储
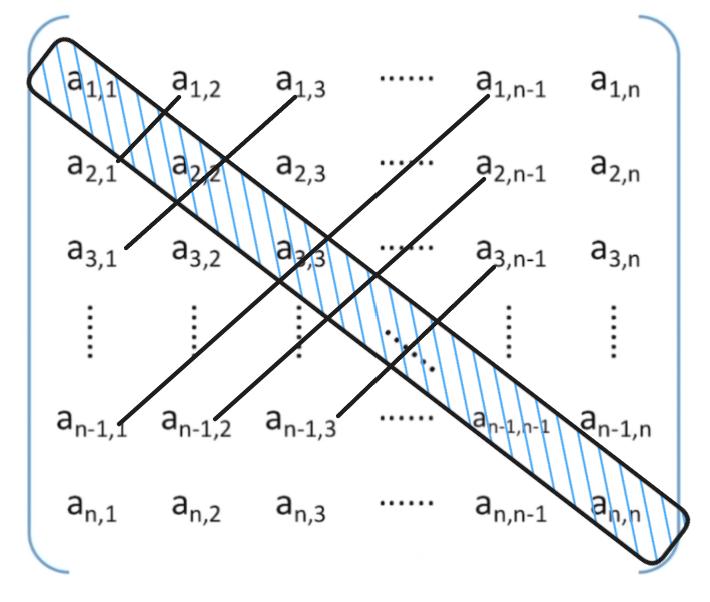
若n阶矩阵任意一个元素**ai,j都有ai,j = aj,i**,则称该矩阵为 对称矩阵
普通存储: n*n二维数组
压缩存储:只存储主对角线 + 下三角(主对角线 + 上三角),也就是按照行优先的原则,按照下图顺序存储。(这里的下三角和上三角就是指以对角线为界限的下方和上方区域)
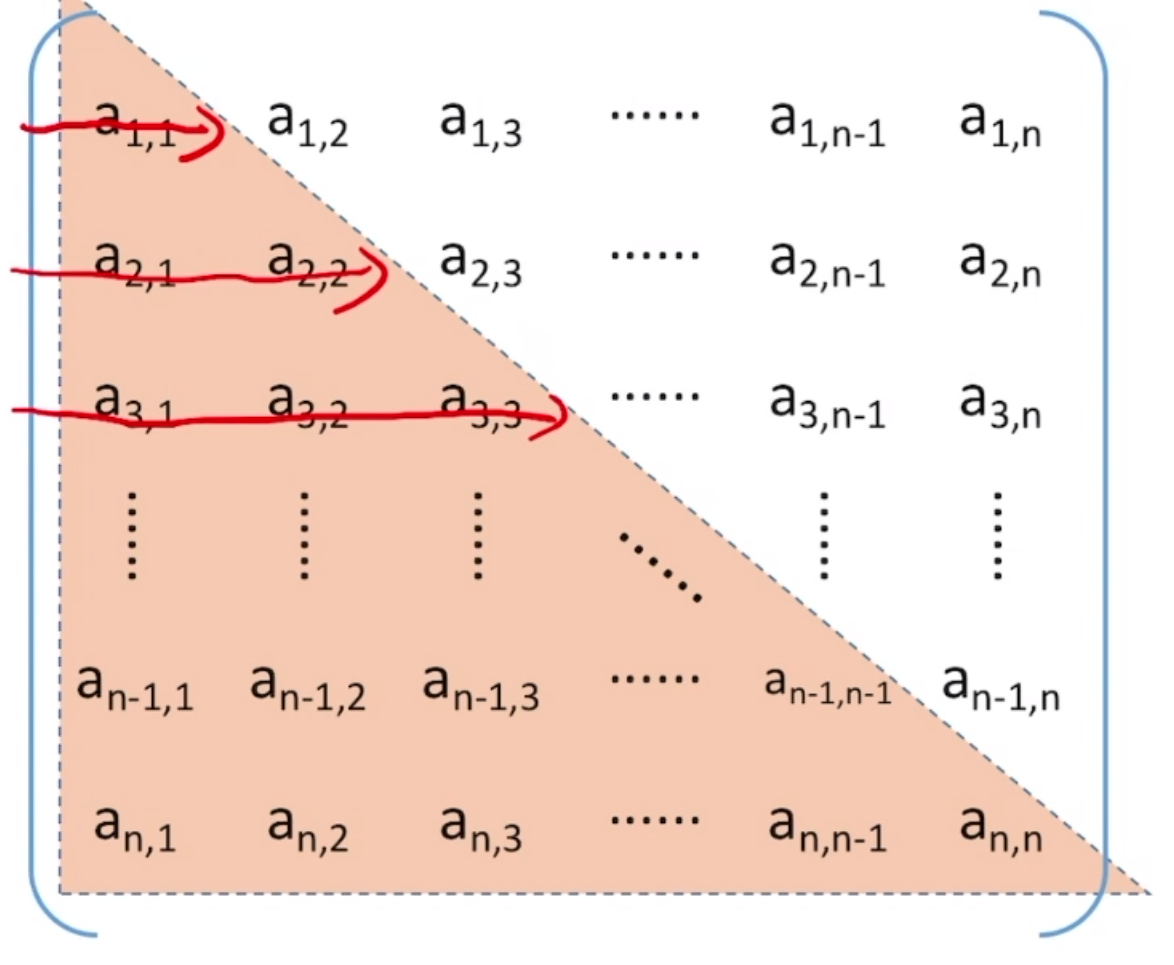
因此这个存储的一维数组的大小就是 1 + 2 + 3 + … + n = (1 + n) * n / 2,但是这样存储的数组不方便观察其数组元素在矩阵中对应的位置,这里我们可以实现一个“映射” 函数=,将矩阵下标**->** 一维数组下标。这个地方是很简单的。
按照行优先原则: ai,j 是第i * (i - 1) / 2 + j 个元素,下标就是 i * (i - 1) / 2 + j - 1 这些东西是不可以直接死记硬背的,应该在考场中可以直接推导的,而且公式一般最后推出来也不是前面写的公式,题目肯定会稍微有些改动的。
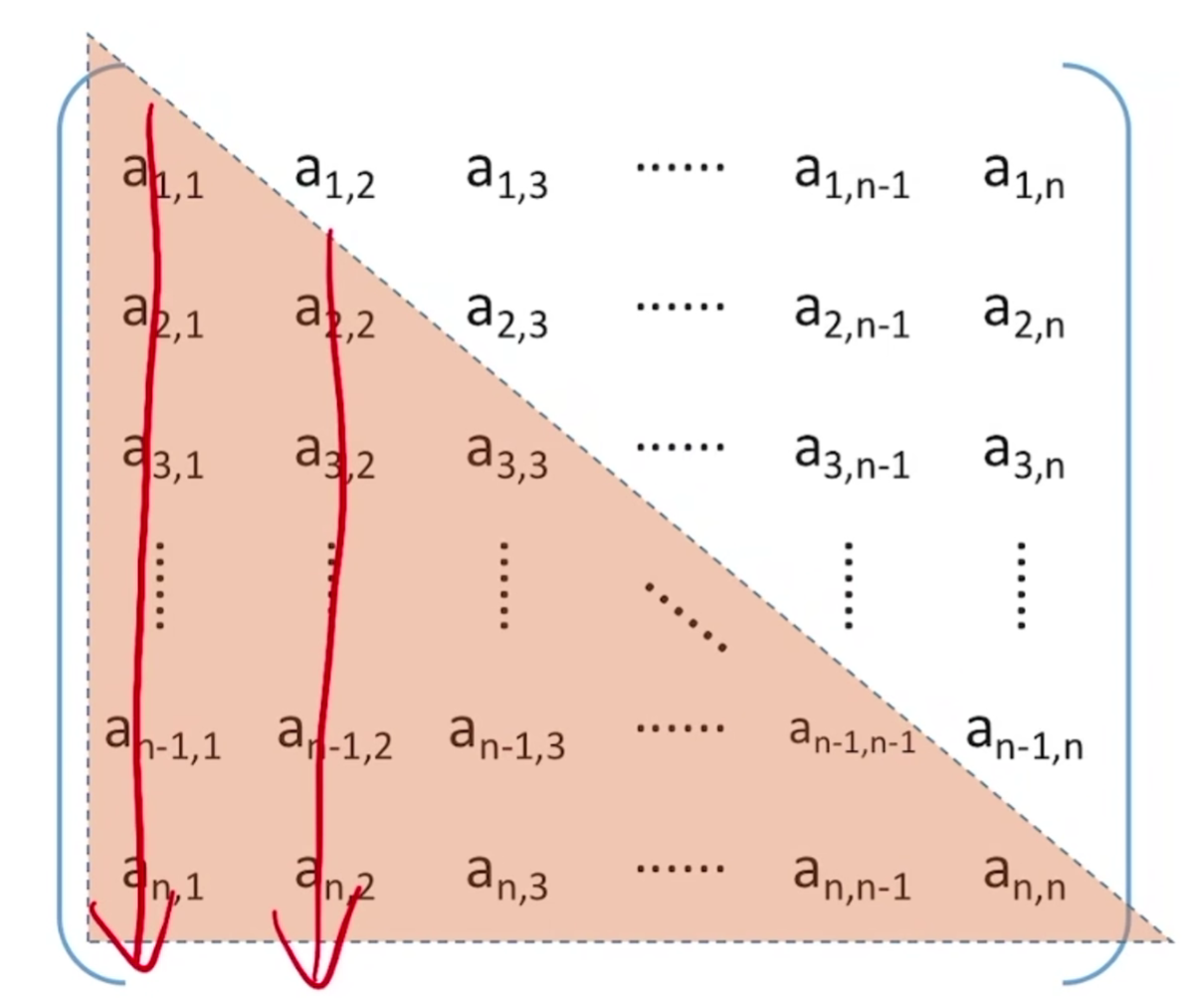
按照行优先原则: ai,j 是第**[n + n - 1 + … + (n - j + 2)] + (i - j) + 1** 个元素。但是像这种公式推理毫无意义,最好现推。
三角矩阵的压缩存储
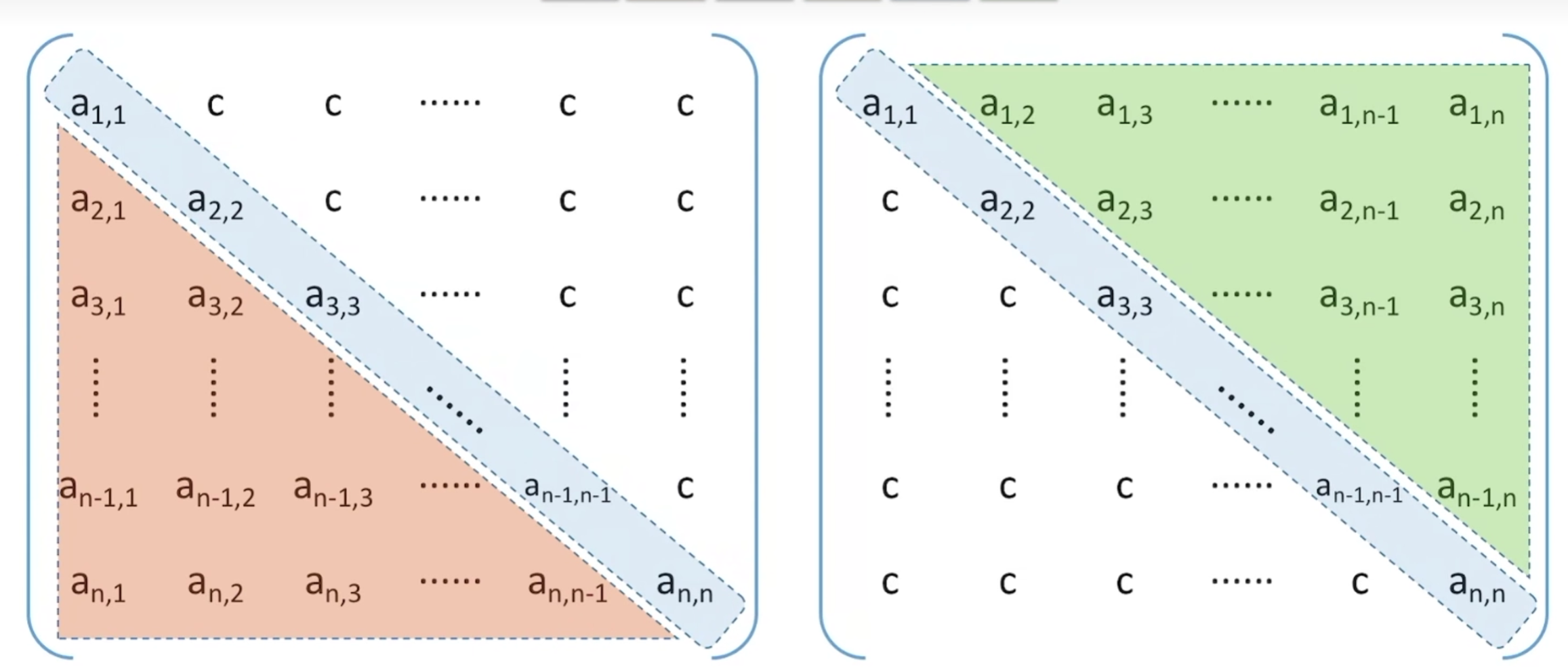
直接看图,上三角或者下三角全部都是一个常数的矩阵
下三角矩阵按照行优先原则存储方式:

三对角矩阵(带状矩阵)的压缩存储

可以直白地理解为中间的三条对角线可以为非0元素的矩阵
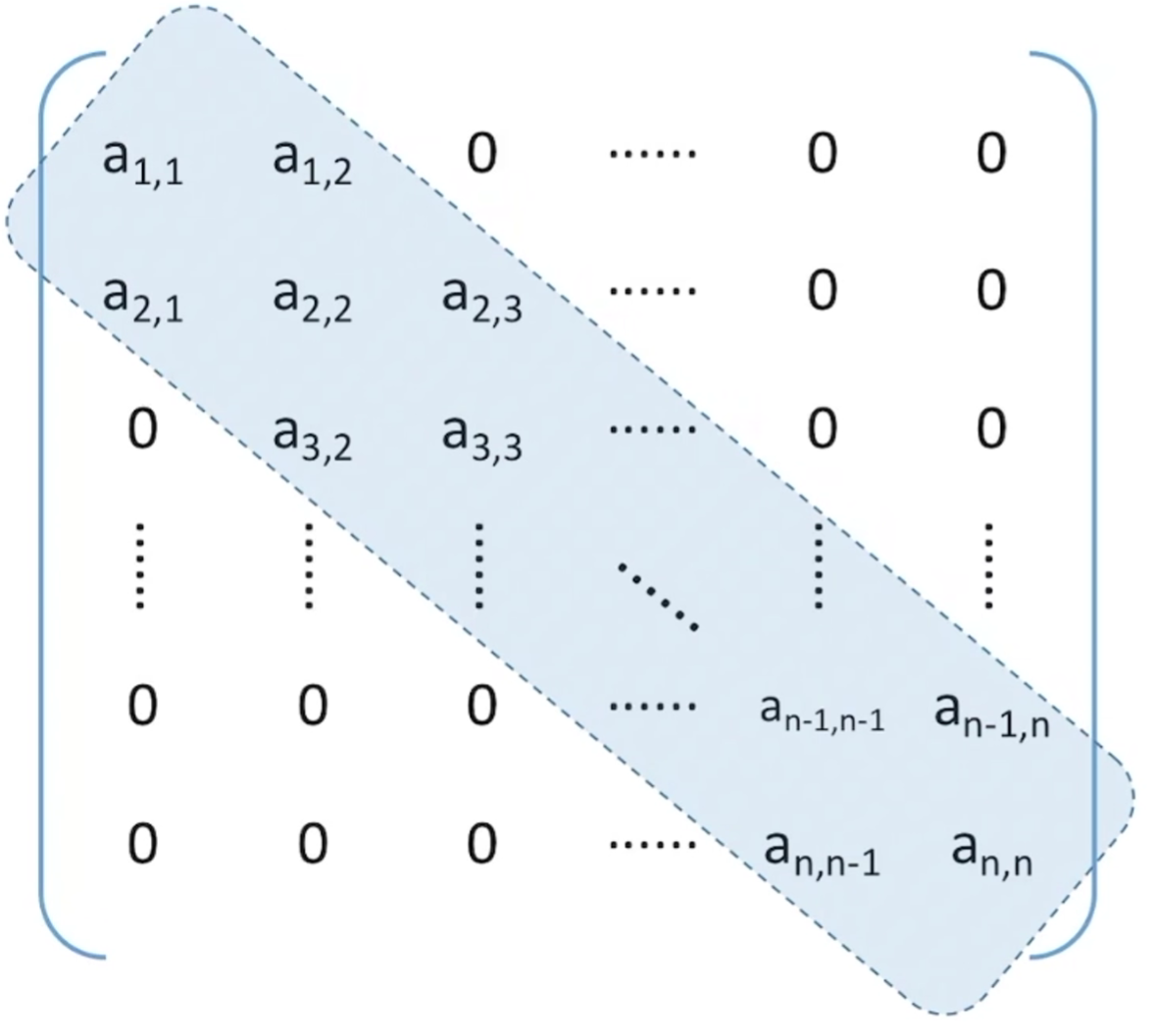
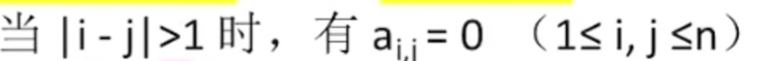
接下来同样地按照行优先原则来存储就是按照a1,1 ,a1,2 ,a2,1,a2,2,a2,3 ,…,an,n 这样的顺序进行存储压缩存储。存储元素的个数就是n + n - 1 + n - 1 = 3n - 2 ,数组下标为 0~3n-3

直接王道讲解

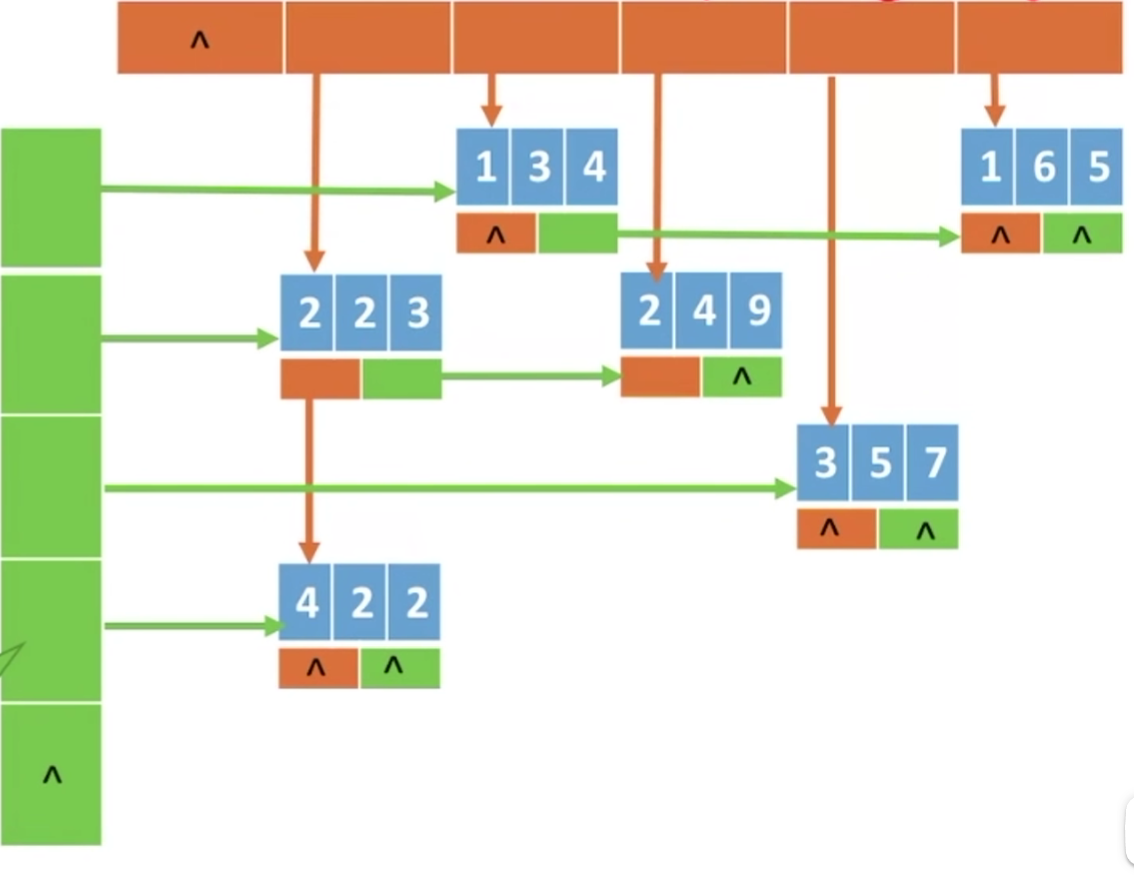
稀疏矩阵的压缩存储
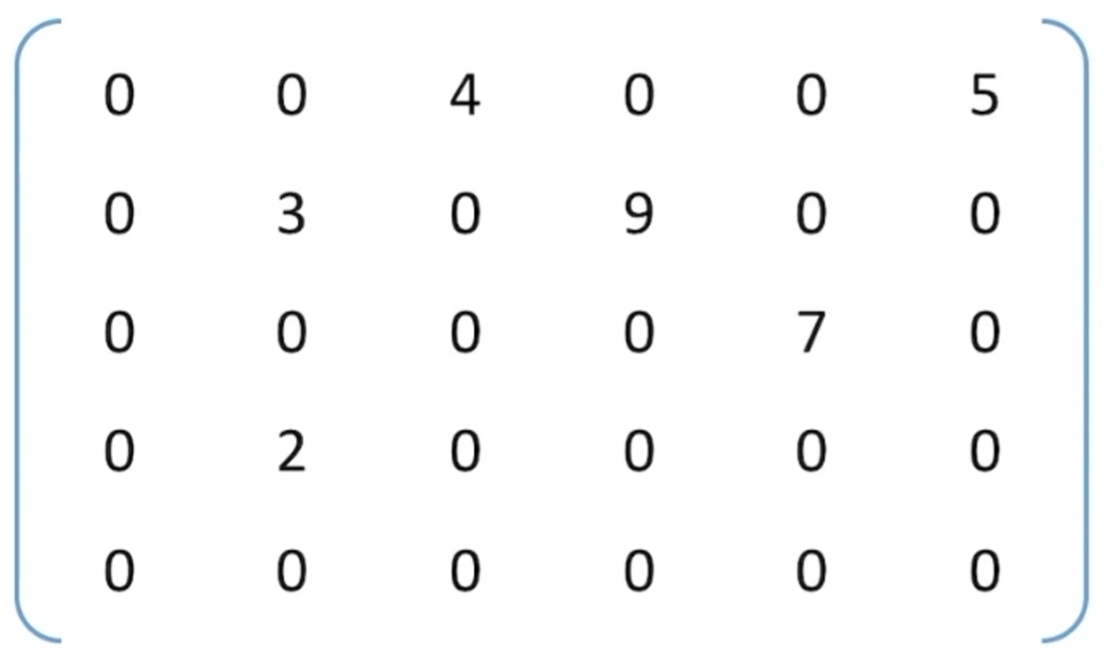
非零元素远远少于矩阵元素的个数。

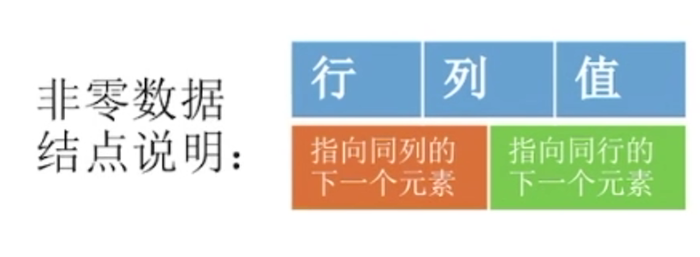
方式一:顺序存储——三元组<行,列,值>
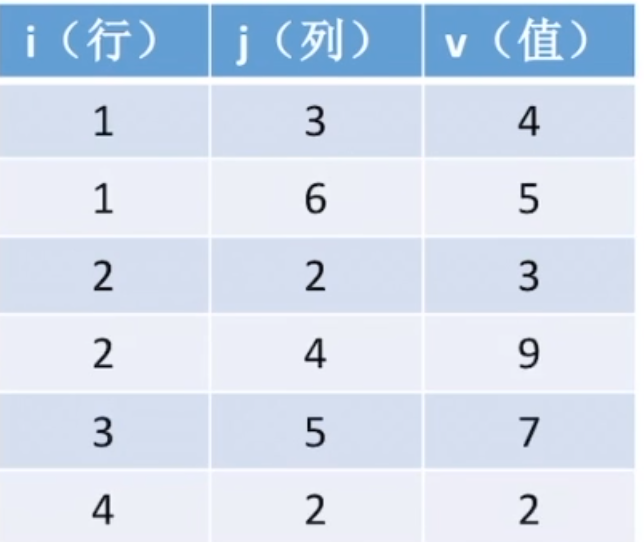
方式二:十字链表法(这个部分很重要,先在这里打个标记,之后我会找时间写一小节来进行讲解)