算法学习专栏——三分法
前言
证明
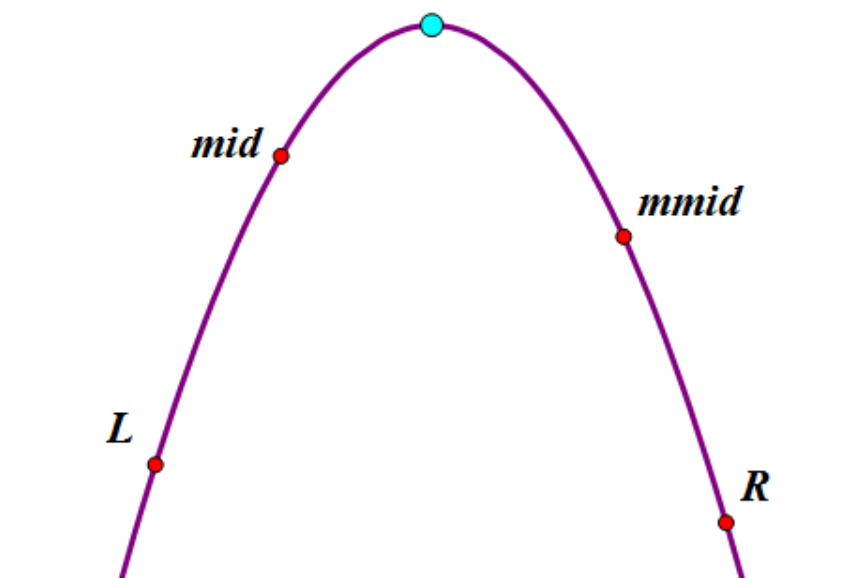
已知:左右端点L、R,要求找到上图中空心点的位置
思路:通过不断缩小 [L,R] 的范围,无限逼近空心点
思想:先取 [L,R] 的中点 mid,再取 [mid,R] 的中点 mmid,通过比较 f(mid) 与 f(mmid) 的大小来缩小范围。
当最后 L=R-1 时,再比较下这两个点的值,我们就找到了答案。
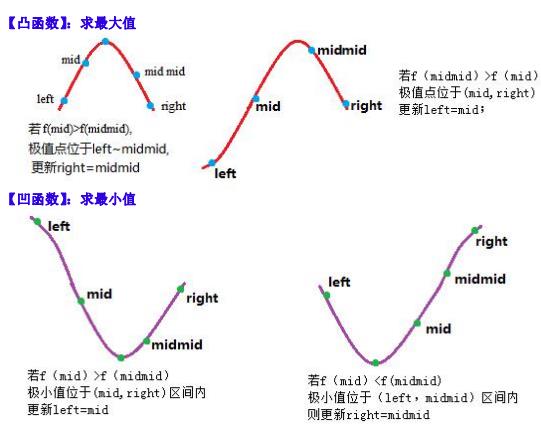
1、当 f(mid) > f(mmid) 的时候,我们可以断定 mmid 一定在空心点的右边。
反证法:假设 mmid 在白点的左边,则 mid 也一定在白点的左边,又由 f(mid) > f(mmid) 可推出 mmid < mid,与已知矛盾,故假设不成立。
所以,此时可以将 R = mmid 来缩小范围。
2、当 f(mid) < f(mmid) 的时候,我们可以断定 mid 一定在空心点的左边。
反证法:假设 mid 在白点的右边,则 mmid 也一定在白点的右边,又由 f(mid) < f(mmid) 可推出 mid > mmid,与已知矛盾,故假设不成立。
同理,此时可以将 L = mid 来缩小范围
转载于:https://blog.csdn.net/lylzsx20172018/article/details/101900805
模版
凹函数
1 | |
凸函数和凹函数统一
1 | |
一、三分(凸函数)(简单+)
题目描述
如题,给出一个 $N$ 次函数,保证在范围 $[l, r]$ 内存在一点 $x$,使得 $[l, x]$ 上单调增,$[x, r]$ 上单调减。试求出 $x$ 的值。
输入格式
第一行一次包含一个正整数 $N$ 和两个实数 $l, r$,含义如题目描述所示。
第二行包含 $N + 1$ 个实数,从高到低依次表示该 $N$ 次函数各项的系数。
输出格式
输出为一行,包含一个实数,即为 $x$ 的值。若你的答案满足以下二者之一,则算正确:
- 你的答案 $x’$ 与标准答案 $x$ 的相对或绝对误差不超过 $10^{-5}$。
- 你的答案 $x’$ 与标准答案 $x$ 对应的函数值,即 $f(x’) $ 和 $f(x)$ 的相对或绝对误差不超过 $10^{-5}$。
样例 #1
样例输入 #1
1 | |
样例输出 #1
1 | |
提示
对于 $100%$ 的数据,$6 \le N \le 13$,函数系数均在 $[-100,100]$ 内且至多 $15$ 位小数,$|l|,|r|\leq 10$ 且至多 $15$ 位小数。$l\leq r$。
【样例解释】
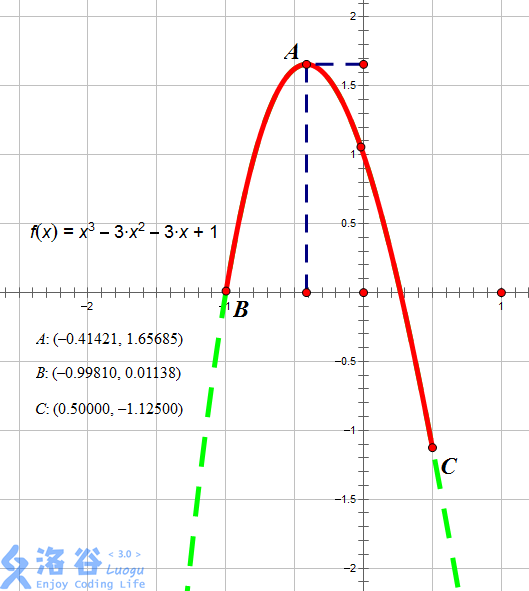
如图所示,红色段即为该函数 $f(x) = x^3 - 3 x^2 - 3x + 1$ 在区间 $[-0.9981, 0.5]$ 上的图像。
当 $x = -0.41421$ 时图像位于最高点,故此时函数在 $[l, x]$ 上单调增,$[x, r]$ 上单调减,故 $x = -0.41421$,输出 $-0.41421$。
思路
二分查找适用于单调函数中逼近求解某点的值。如果遇到凸性或凹形函数时,可以用三分查找求此凸点或凹点。
代码
答案(请自己先思考一下再参考)
#include < iostream>
#include < cstdio>
using namespace std;
const int N = 15;
#define eps 1e-7
int n;
double l,r;
double a[N]; // 系数
double check(double x)
{
double ans = 1, sum = 0;
for(int i = n + 1 ;i >= 1;i -- )
{
sum += ans * a[i];
ans *= x;
}
return sum;
}
int main()
{
cin >> n >> l >> r;
for(int i = 1;i <= n + 1;i ++ ) cin >> a[i];
while(r - l > eps)
{
double mid = (l + r) / 2;
double mmid = (mid + r) / 2;
if(check(mid) > check(mmid) ) r = mmid;
else l = mid;
}
printf("%.5lf",l);
return 0;
}
二、货仓选址(凹函数)(简单+)
在一条数轴上有 N 家商店,它们的坐标分别为 A1∼AN。
现在需要在数轴上建立一家货仓,每天清晨,从货仓到每家商店都要运送一车商品。
为了提高效率,求把货仓建在何处,可以使得货仓到每家商店的距离之和最小。
输入格式
第一行输入整数 N。
第二行 N 个整数 A1∼AN。
输出格式
输出一个整数,表示距离之和的最小值。
数据范围
1≤N≤100000
0≤Ai≤400000
输入样例:
1 | |
输出样例:
1 | |
思路
代码
答案(请自己先思考一下再参考)
#include < iostream>
#include < algorithm>
using namespace std;
const int N = 100010;
int n;
int a[N];
int check(int x)
{
int res = 0;
for(int i = 0 ;i < n;i ++ ) res += abs(a[i] - x);
return res;
}
int main()
{
cin >> n;
for(int i = 0 ;i < n;i ++ ) cin >> a[i];
sort(a, a + n);
int l = a[0], r = a[n - 1];
while(l < r - 1) // l < r - 1 ?
{
int mid = (l + r) / 2;
int mmid = (mid + r) / 2;
if(check(mid) > check(mmid)) l = mid;
else r = mmid;
}
cout << min(check(l),check(r)) << endl;
return 0;
}
三、曲线
明明做作业的时候遇到了 n 个二次函数 Si(x)=ax^2^+bx+c,他突发奇想设计了一个新的函数 F(x)=max{Si(x)},i=1…n。
明明现在想求这个函数在 [0,1000] 的最小值,要求精确到小数点后四位,四舍五入。
输入格式
输入包含 T 组数据,每组第一行一个整数 n;
接下来 n 行,每行 3 个整数 a,b,c,用来表示每个二次函数的 3 个系数。注意:二次函数有可能退化成一次。
输出格式
每组数据输出一行,表示新函数 F(x)() 的在区间 [0,1000] 上的最小值。精确到小数点后四位,四舍五入。
数据范围
1≤T≤10
1≤n≤10^5^
0≤a≤1000≤≤100,
0≤|b|,|c|≤50000
输入样例:
1 | |
输出样例:
1 | |
思路
代码
答案(请自己先思考一下再参考)
#include < bits/stdc++.h>
using namespace std;
const double eps = 1e-8; // eps尽量开高,不然会WA
const int N = 100010;
int n, a[N], b[N], c[N];
double check(double x)
{
double res = -1e9;
for (int i = 1; i <= n; i++) res = max(res, a[i] * x * x + b[i] * x + c[i]);
return res;
}
int main()
{
int t; cin >> t;
while (t--)
{
cin >> n;
for (int i = 1; i <= n; i++) cin >> a[i] >> b[i] >> c[i];
double l = 0, r = 1000;
while (r - l >= eps)
{
double mid = (l + r) / 2;
double mmid = (mid + r) / 2;
if (check(mid) >= check(mmid)) l = mid;
else r = mmid;
}
printf("%.4lf\n", check(r));
}
return 0;
}