算法练习专栏Acwing周赛练习第147场周赛

A：平衡数组（简单）

5555. 平衡数组 - AcWing题库

给定一个长度为 n 的整数数组 a1,a2,…,an。

如果一个整数数组恰好包含相同数量的奇数元素和偶数元素，就称该数组为一个平衡数组。

请你判断数组 a 是否是一个平衡数组。

保证 n 是偶数。

输入格式

第一行包含整数 n。

第二行包含 n 个整数 a1,a2,…,an。

输出格式

如果数组 a 是平衡数组，则输出 Yes，否则，输出 No。

数据范围

前 3 个测试点满足 2≤n≤10。
所有测试点满足 2≤n≤100，1≤ai≤100。

输入样例1：

1 2	`6 1 2 3 4 5 6`

输出样例1：

Yes

输入样例2：

1 2	`6 1 2 3 4 5 7`

输出样例2：

No

代码

#include <iostream>
using namespace std;
const int N = 110;
int n;

int main()
{
    ios::sync_with_stdio(false),cin .tie(0),cout.tie(0);
    cin >> n;
    int res = 0;
    for (int i = 1; i <= n ;i++) {
        int x;
        cin >> x;
        if (x % 2 == 0) res++;
    }
    if (res == n - res) cout << "Yes";
    else cout << "No";
    
    return 0;
}

B：牛的语言学（困难）

牛语单词通过以下规则构造：

牛语单词仅由小写字母构成。
牛语单词的具体结构为：词根+若干个（个或更多）后缀，其中：
- 词根为长度大于 4 的字符串。
- 后缀为长度 2 或 3 的字符串。
在构成单词时，不允许连续两次（或更多次）添加同一后缀。

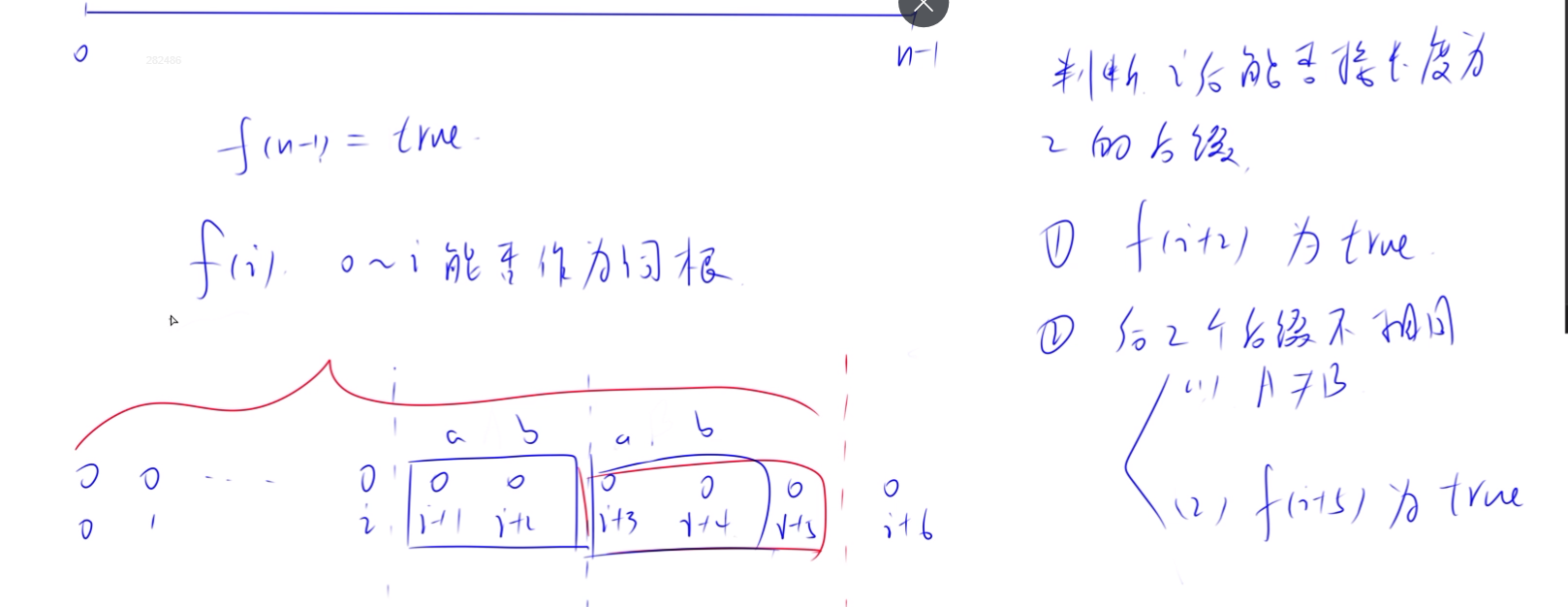
给定一个已经构造好的牛语单词 s，请你根据牛语单词的构造规则，找到该单词的所有可能后缀。

例如，如果给定单词为 cbcaabaca，则它可能的构造方式为 cbcaabaca、cbcaaba+ca、cbcaab+aca、cbcaa+ba+ca，因此，它的所有可能后缀为 aca,ba,ca。

输入格式

一个由小写字母构成的字符串 s。

输出格式

第一行输出整数 k，表示单词 s 的所有可能后缀的数量。

接下来 k 行，按照字典序每行输出一个可能后缀。

数据范围

前 3 个测试点满足 5≤|s|≤10^5^。
所有测试点满足 5≤|s|≤10^4^。

输入样例1：

1	`cbcaabaca`

输出样例1：

3
aca
ba
ca

输入样例2：

abaca

输出样例2：

思路

可以通过链接看看 y 总的讲解

代码(DP)

#include <iostream>
#include <cstring>
#include <algorithm>
#include <set>

using namespace std;

const int N = 10010;

int n;
string s;
bool f[N];

int main()
{
    cin >> s;
    n = s.size();

    f[n - 1] = true;
    set<string> res;
    for (int i = n - 2; i >= 4; i -- )
        for (int j = 2; j <= 3; j ++ )
            if (f[i + j])
            {
                string a = s.substr(i + 1, j);
                string b = s.substr(i + 1 + j, j);
                if (a != b || f[i + 5])
                {
                    f[i] = true;
                    res.insert(a);
                }
            }

    cout << res.size() << endl;
    for (auto& t: res) cout << t << endl;

    return 0;
}

C：孤立点数量（中等）

5557. 孤立点数量 - AcWing题库

给定一个 n 个点 m 条边的无向图。

图中没有重边和自环。

不保证给定图是连通图。

现在，你需要给图中的每一条边定向，使得给定图变为一个有向图。

我们规定，如果一个点的入度为 0，则称其为孤立点。

我们希望改造后的有向图中孤立点的数量尽可能少。

输出孤立点的最少可能数量。

输入格式

第一行包含两个整数 n,m,。

接下来 m 行，每行包含两个整数 xi,yi,，表示点 xi 和点 yi 之间存在一条边。

输出格式

一个整数，表示孤立点的最少可能数量。

数据范围

前 4 个测试点满足 2≤n≤10，1≤m≤10。
所有测试点满足 2≤n≤10^5^，1≤m≤10^5^，1≤xi,yi≤n，xi≠yi。

输入样例1：

输出样例1：

输入样例2：

输出样例2：

输入样例3：

输出样例3：

思路

可以看看y总的视频，可知结论：如果一个集合中出现环，这个集合点的孤立点的数量就为0

一个集合没有环孤立点就为1

如何判断连通块内有没有环呢？
第一步：分连通块，用并查集
第二步：判断环，由于这题没有重边，所以点数 = 边数 + 1 则没有环，反之有环

代码(并查集)

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 100010;

int n, m;
int p[N];
bool st[N];

int find(int x)
{
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++ ) p[i] = i;

    while (m -- )
    {
        int a, b;
        scanf("%d%d", &a, &b);
        a = find(a), b = find(b);
        if (a == b) st[a] = true; // 如果两个点在一个集合里的话，那么意味着是会成环的
        else p[a] = b, st[b] |= st[a]; // 如果不同就加到一个集合里去呗
    }

    int res = 0;
    for (int i = 1; i <= n; i ++ )
        if (p[i] == i && !st[i])
            res ++ ;

    printf("%d\n", res);
    return 0;
}

8、算法练习专栏——牛客练习—-牛客小白月赛88 上一篇

算法练习专栏——Acwing周赛练习——第146场周赛下一篇