算法学习专栏——深度优先遍历+BFS

前言

大家大概率是还没有接触到图的概念的，所以我这里先简单简单介绍一下图的基本概念。

图是什么？图实际上就是多个地点之间连线和地点的集合。

没看懂，再说清楚点，看下图：

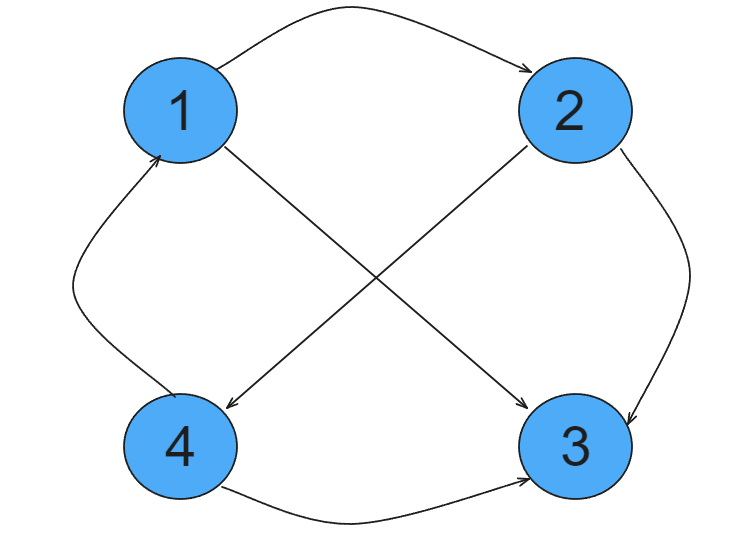
像这样一张图，可以看做一个标准的图。有箭头的图（两个点直接有方向性，就以上图为例，1可以到2,但是2不可以到1），就是有向图。 反之没有箭头（这样两个地方就是互通的，可以双向走）。

上面的一点点内容弄懂了就可以往下看了。

一、走迷宫（BFS）（简单+）

给定一个 n×m 的二维整数数组，用来表示一个迷宫，数组中只包含 0或 1，其中 0 表示可以走的路，1 表示不可通过的墙壁。

最初，有一个人位于左上角 (1,1) 处，已知该人每次可以向上、下、左、右任意一个方向移动一个位置。

请问，该人从左上角移动至右下角 (n,m) 处，至少需要移动多少次。

数据保证 (1,1) 处和 (n,m) 处的数字为 0，且一定至少存在一条通路。

输入格式

第一行包含两个整数 n 和 m。

接下来 n 行，每行包含 m 个整数（0 或 1），表示完整的二维数组迷宫。

输出格式

输出一个整数，表示从左上角移动至右下角的最少移动次数。

数据范围

1≤n,m≤100

输入样例：

输出样例：

思路

代码

答案（请自己先思考一下再参考）

        
#include < iostream>
#include < cstring>
#include < cstdio>
#include < algorithm>
using namespace std;
const int N = 110;
typedef pair< int, int> PII;
int n, m;
int a[N][N],vis[N][N];
PII q[N * N];
int bfs()
{
    int hh = 0, tt = 0; 
    memset(vis,-1, sizeof vis);  
    vis[1][1] = 0;
    q[0] = {1, 1};
    int dx[4] = {1,0,-1,0},dy[4] = {0,1,0,-1};   
    while (hh <= tt)
    {
        auto t = q[hh++];
        for (int i = 0; i < 4; i++)
        {
            int x = t.first + dx[i],y = t.second + dy[i];
            if (x >= 1 && x <= n && y >= 1 && y <= m && vis[x][y] == -1 && a[x][y] == 0)
            {
                vis[x][y] = vis[t.first][t.second] + 1;
                q[++tt] = {x, y};                
            }
        }
    }
    return vis[n][m];
}
int main()
{
    ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            cin >> a[i][j];  
    cout << bfs();    
    return 0;
}

三、树的重心（深度优先遍历）（中等-）

给定一颗树，树中包含 n 个结点（编号 1∼n）和 n−1 条无向边。

请你找到树的重心，并输出将重心删除后，剩余各个连通块中点数的最大值。

重心定义：重心是指树中的一个结点，如果将这个点删除后，剩余各个连通块中点数的最大值最小，那么这个节点被称为树的重心。

输入格式

第一行包含整数 n，表示树的结点数。

接下来 n−1 行，每行包含两个整数 a 和 b，表示点 a 和点 b 之间存在一条边。

输出格式

输出一个整数 m，表示将重心删除后，剩余各个连通块中点数的最大值。

数据范围

1≤n≤10^5^

输入样例

输出样例：

思路（！！！）

代码

答案（请自己先思考一下再参考）

        
#include < iostream>
#include < algorithm>
#include < cstring>
using namespace std;
const int N = 1e5 + 10, M = N * 2;
int e[M],ne[M],h[N],idx;
int n;
bool st[N];
int ans = N;
void add(int x,int y)
{
    e[idx] = y,ne[idx] = h[x],h[x] = idx++;
}
int dfs(int x)
{
    st[x] = true;   
    int res = 0,sum = 1;
    for (int i = h[x]; i != -1; i = ne[i])
    {
        int j = e[i];
        if (!st[j])
        {
            int t = dfs(j);
            res = max(res, t);
            sum += t;
        }
    }    
    res = max(res,n - sum);
    ans = min(res, ans);   
    return sum;
}
int main()
{
    ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
    cin >> n;
    memset(h, -1, sizeof h);
    for (int i = 0; i < n - 1; i++)
    {
        int x, y;
        cin >> x >> y;
        add(x, y),add(y, x);
    }   
    dfs(1);   
    cout << ans;
    return 0;
}

算法学习专栏——广度优先遍历上一篇

算法学习专栏——递归（DFS）下一篇