算法练习专栏算法小扩展01——秦九昭算法(选看)
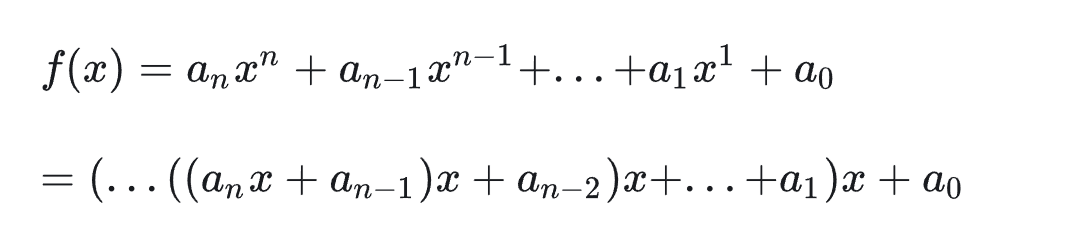
题目描述
秦九韶算法是中国南宋时期的数学家秦九韶提出的一种多项式简化算法。
对于一个一元次多项式:
在代入一个特定的进行整体求值时,若用朴素方法处理,需要经过


秦九韶算法的中心思想:

改写为



输入
第1行输入
第2行输,



第3行输入
输出
一行,表示上述的值。
分析
用朴素方法处理的值时,计算




1.答案

2.对于




3.输出结果
代码
1 | |
(a1)
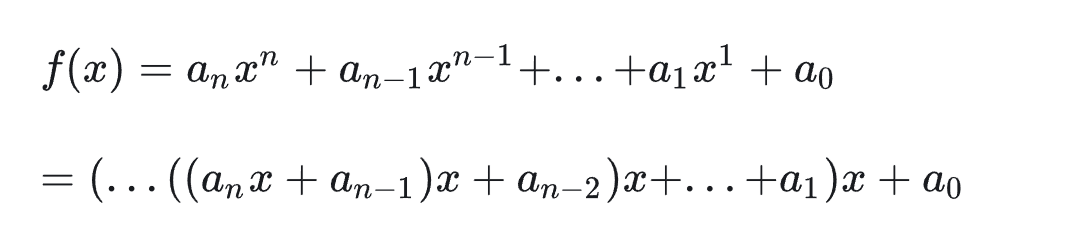
秦九韶算法是中国南宋时期的数学家秦九韶提出的一种多项式简化算法。
对于一个一元次多项式:
在代入一个特定的进行整体求值时,若用朴素方法处理,需要经过


秦九韶算法的中心思想:

改写为



第1行输入
第2行输,



第3行输入
一行,表示上述的值。
用朴素方法处理的值时,计算




1.答案

2.对于




3.输出结果
1 | |
(a1)