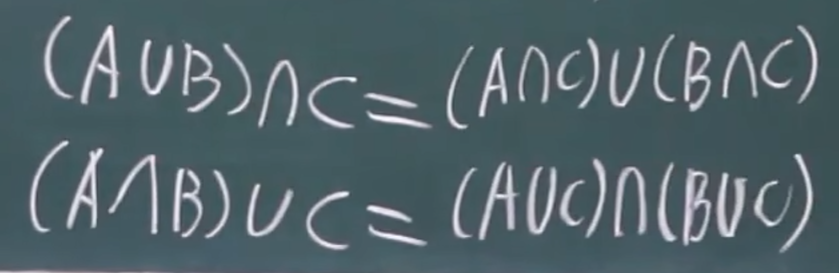2、概率论——事件间的关系
包含关系
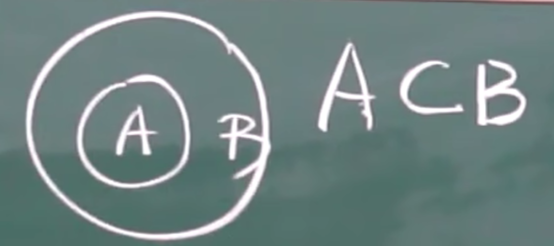A必然导致B发生。
相等：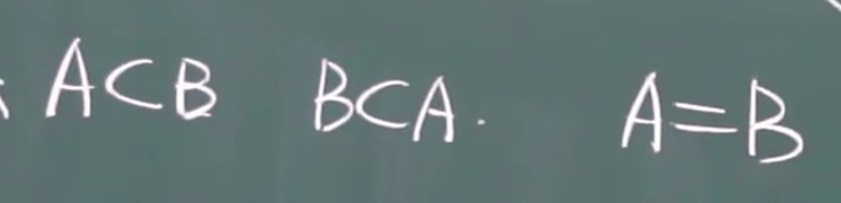 
并（和）
A U B，A + B
A、B事件至少一个发生。
交（积）
A ^ B, AB
A、B事件同时发生
无限可列个
按某种规律排成一个序列
自然数：1,2，3,4,5,6……
整数： 0,1，-1,2，-2，……
有理数：
但是比如说： 实数、直线点集等是不可列的，排不成一个队
差
A - B，A发生，B不发生，属于A但是不属于B
A - B = A - AB
互不相容事件
A、B不同时发生，AB =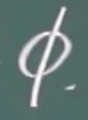 
n个事件A1,A2,A3….An，AiAj = 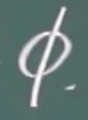这就叫做两两互不相容
对立事件
A、B互不相容且AUB=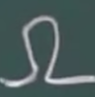
AB = 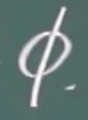且 A + B =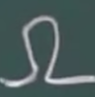
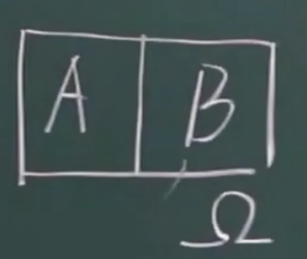
表示事件A的逆。
A - B = A - AB =
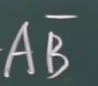
联系和区别
- 两事件对立，则一定是互不相容的。
- 互不相容适用于多个事件。
- 对立只适用于两个事件之间。
- 互不相容代表着不能同时发生，可以都不发生。
- 对立事件： 有且仅有一个发生
完备事件组
A1，A2，A3……An两两不相容，且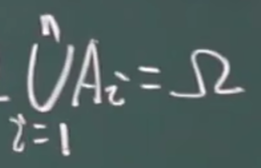
运算律
- 交换律……
- 结合律……
- 分配律：
对偶律
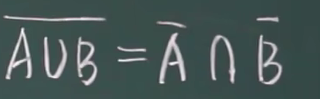
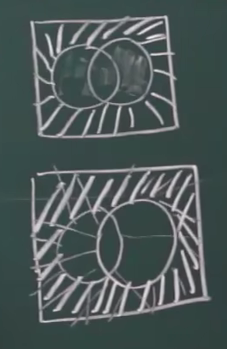
例题1
例题2
