杂题——How many answers are wrong

How many answers are wrong

​ FF是个熊男孩，他总是恳求TT和他一起玩接下来的游戏。
​ 这是一个非常无聊的游戏：首先，TT写下一个整数序列。然后，FF从中选择一个连续的子序列（例如，从第3个整数到第5个整数的子序列），问TT他选择的 子序列的和是多少？接下来，TT将回答FF的问题。然后，重复这个过程，直到FF算出整个整数序列的和。

​ 这真是一个非常非常无聊的游戏！TT根本不想和FF玩。为了惩罚FF，她经常故意告诉FF错误的答案。

​ 熊男孩不是笨男孩。FF能够发现TT说的一些答案是不兼容的。当然，这些矛盾使得计算序列和变得困难。

​ 然而，TT是一个很好的和可爱的女孩。她不忍心对FF太苛刻。为了节省时间，她保证在没有逻辑错误的情况下，答案都是正确的。

​ 而且，如果FF发现一个答案是错误的，他会在判断下一个答案时忽略它。

​ 但因为有太多的问题，可怜的FF一时无法确定当前的答案是对还是错。所以他决定写一个程序来帮助他解决这个问题。该程序将可以接收FF提出的一系列问题，以及FF从TT收到的答案。这个程序的目的是找出有多少答案是错误的。只有忽略错误的答案，FF才能算出整个整数序列。

【输入格式】

​ 第1行：两个整数N和M (1<=N<=200000, 1<=M<= 40000)。表示TT写了N个整数，FF问了她M个问题。
​ 第2行到第M+1行：每行包含三个整数Ai，Bi和Si。表示TT回答FF从第Ai个整数到第Bi个整数的和是Si，且保证0<Ai<= Bi<= N。

【输出格式】

​ 一个整数：表示有多少个答案是错误的。

【输入输出样例】

输入

1
2
3
4
5
6
10 5
1 10 100
7 10 28
1 3 32
4 6 41
6 6 1

输出：

1
1

思路

​ 题意转换：这道题目可以转换为求解这么一个问题：输入m组数据，每输入一组我们就需要判断是否与前面冲突，最后我们需要输出冲突数据的个数。不合理的情况有比如说：先给出[1,5]，区间和为100;再给出区间[3,5]为50,最后给出区间 [1,2]为200，肯定有冲突。

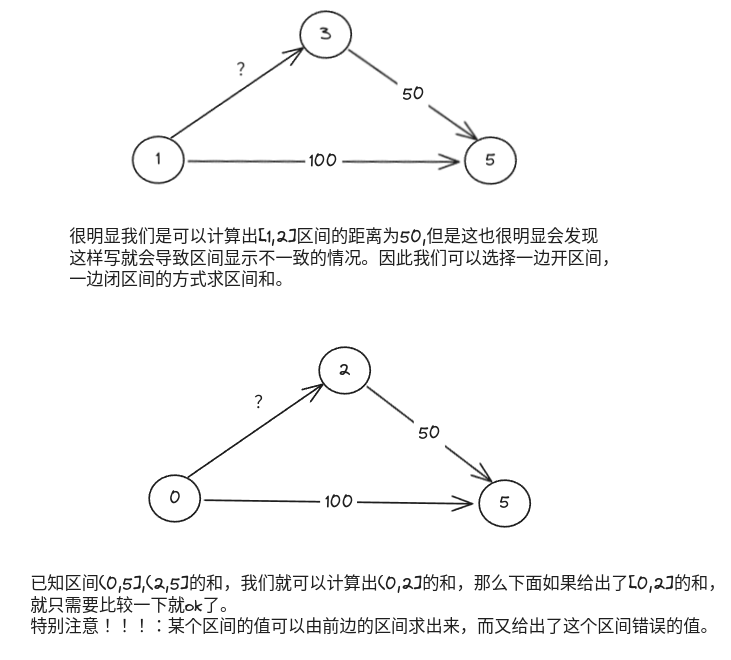
​ 基本思路： 这道题目我们将使用到带权并查集经典思路，**核心思路就是维护多个元素之间的联通以及偏移关系**。在处理上一般的并查集问题和带权并查集问题的唯一区别就是需要存储每个集合中各个节点到根节点的位置，其他基本一致。下面就详细说一说这道题目的思路吧：

​ 这道题目我们要明白这个题目怎么就可以使用并查集这个算法呢？请看下图：

image-20240426182432912

​ 最终这道题目用人话说的基本思路还是并查集的基本思路：

​ 如果给定区间的两个端点属于同一个并查集，判断这个区间的值是否与计算得到的值相等；如果给定区间的两个端点不属于同一个并查集，将这两个并查集合并。并查集边的权值就等于题干中的区间和。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
#define _CRT_SECURE_NO_WARNINGS
 
#include <iostream>
#include <stdio.h>
using namespace std;
 
const int maxM = 200005;
int parent[maxM];
int sum[maxM];
 
int Find(int x)
{
	if (x != parent[x])
	{
		int i = parent[x];
		parent[x] = Find(parent[x]);
		sum[x] += sum[i];
	}
	return parent[x];
}
 
 
int main()
{
	int m, n;
	int ans = 0;
	while (scanf("%d%d", &m, &n) != EOF)
	{
		for (int i = 0; i <= m; i++)
		{
			parent[i] = i;
			sum[i] = 0;
		}
		ans = 0;
		while (n--)
		{
			int l, r, value;
			cin >> l >> r >> value;
			l--;
			int fl = Find(l);
			int fr = Find(r);
			if (fl == fr)
			{
				if ((sum[l] - sum[r]) != value)
				{
					ans++;
				}
			}
			else {
				parent[fl] = fr;
				sum[fl] = -sum[l] + sum[r] + value;
			}
		}
		cout << ans << endl;
	}
	return 0;
}