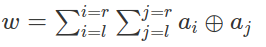算法练习专栏——牛客练习——牛客练习赛124内测(炼狱难度)

A：智乃的gcd构造

链接

题目描述

智乃想让你构造两个正整数a,b，满足

image-20240422213036170
其中|x∣表示求绝对值，gcd(a,b)表示求a和b的最大公因数。

输入描述:

1
仅一行，三个正整数x,y,z(1≤x,y,z≤1018)。

输出描述:

1
2
3
请构造任意满足题目要求的a,b∈[1,5×1018]。

可以证明总是存在这样的答案。

示例1

输入

复制

1
284 1136 142

输出

复制

1
426 710

说明

1
2
3
710−426=284
710+426=1136
gcd(426,710)=142

思路

​ 思路一：就是首先进行埃式筛法选出1e7内的所有质数，然后再将a=z,然后bX这些质数一直乘到符合条件为止，这个思路思维上应该是不存在问题的，但是不够。

​ 思路二：一步即可。

代码一（错误代码）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
#include <iostream>
#include <cmath>

using namespace std;

unsigned long long x, y, z, a, b;
const int N = 1e7 + 10;
unsigned long long primes[N];
bool st[N];
int k = 0;
unsigned long long aa, bb;

void prime() {
    for (int i = 2; i <= N; i++) {
        if (!st[i]) {
            primes[k++] = i;
            for (int j = i; j <= N; j += i) st[j] = true;
        } 
    }
}

unsigned long long abss(unsigned long long a, unsigned long long b) {
    if (a >= b) return a - b;
    else return b - a;
}
int main()
{
    int k1, k2;
    cin >> x >> y >> z;
    a = ceil((x + y) / 2.0);
    b = ceil((y - x) / 2.0);
//     cout << a << " "  << b << '\n';
    prime();
//     unsigned long long res = ;'
    for (int i = 0; i < k; i++) {
        unsigned long long kk = primes[i] * z;
        if (kk >= b) {
            bb = kk;
            break;
        }
    }
    
    for (int i = 0; i < k; i++) {
        unsigned long long kk = primes[i] * z;
//         cout <<kk - a << '\n';
        if (kk >= a) {
            if (abss(kk , bb) >= x && (kk + bb) >= y) {
                aa = kk;
                break;    
            }
        }
    }
    
    cout << aa << " " << bb;
    return 0;
}

代码二（模拟）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
// 代码一
#include <iostream>
#include <cmath>

using namespace std;
typedef unsigned long long ULL;

ULL x, y, z, a, b;
ULL aa, bb;

int main()
{
    int k1, k2;
    cin >> x >> y >> z;
    a = z;
    b = z + ((x + a) / z + 1) * z;
    if (a + b < y) {
        b = b + ((y - a) / z + 1) * z;
    }
    cout << a << " " << b;
    return 0;
}

// 代码二
#include <iostream>
#include <cmath>

using namespace std;
typedef unsigned long long ULL;
const ULL inf = 5e18;

ULL x, y, z, a, b;

int main()
{
    cin >> x >> y >> z;
    
    cout << z << " " << inf / z * z;
    return 0;
}

C：智乃的k线段区间

链接

题目描述

在数轴上有N条线段，第i条线段的左右端点分别为li,ri。

定义一段区间[L,R]包含第i条线段，当且仅当L≤li≤ri≤R。

智乃想要知道L,R∈[1,M]且L≤R时，有多少个区间[L,R]包含至少k条线段。

输入描述:

1
2
3
第一行输入三个正整数N,M,K(1≤K≤N≤105,1≤M≤109)。

接下来N行，每行输入两个正整数li,ri(1≤li≤ri≤M)。

输出描述:

1
仅一行一个非负整数，表示问题的答案。

示例1

输入

复制

1
2
3
4
5
6
7
6 9 3
3 5
4 6
5 7
8 8
8 8
8 8

输出

复制

1
19

说明子集mex

1
2
答案为:
[1,8],[2,8],[3,8],[4,8],[5,8],[6,8],[7,8],[8,8],[1,9],[2,9],[3,9],[4,9],[5,9],[6,9],[7,9],[8,9],[1,7],[2,7],[3,7][1,8],[2,8],[3,8],[4,8],[5,8],[6,8],[7,8],[8,8],[1,9],[2,9],[3,9],[4,9],[5,9],[6,9],[7,9] ,[8,9],[1,7],[2,7],[3,7][1,8],[2,8],[3,8],[4,8],[5,8],[6,8],[7,8],[8,8],[1,9],[2,9],[3,9],[4,9],[5,9],[6,9],[7,9],[8,9],[1,7],[2,7],[3,7]

思路

​ 思路一：我的基本思路就是首先将所有绳子按r来进行sort一下，然后使用滑动窗口维护一个长度为k的队列来维护l的最小值，依次 + 最小值即可（需要细节处理特殊情况，比如右端点一直为1的情况）

​ 思路二：上述思路实际上基本正确下面是一位佬给我提供的思路，首先枚举左端点L，把就是把li小于L的删掉，除了这些线段，其他的就是可行的，然后滑动的时候，需要删掉的左li就把对应的ri也从剩余集合删掉，然后从剩余ri中找第k小。

代码一（错解）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
#include <iostream>
#include <algorithm>
#include <vector>

using namespace std;
typedef pair<int, int> PII;
const int N = 1e5 + 10;
vector<PII> query;
int s[N], q[N];
long long res = 0;
vector<PII> Q;

bool cmp(PII A,PII B) {
    return A.second < B.second || (A.second == B.second && A.first < B.first);
}

int main()
{
    int n, m, k;
    cin >> n >> m >> k;
    for (int i = 1; i <= n; i++) {
        int l, r;
        cin >> l >> r;
        query.push_back({l, r});
    }
    sort(query.begin(),query.end(),cmp);
    
	int hh=0,tt=-1;   
	for(int i=0;i<n;i++)
	{
		if(hh<=tt&&i-k+1>q[hh])
			hh++;
		while(hh<=tt&&query[i].first <= query[q[tt]].first)   
			tt--;
		q[++tt]=i;   
		
		if(i-k+1>=0) Q.push_back({query[q[hh]].first, query[i].second});   
	}
//     int ll = 0;
//     for (auto [a, b] : Q) {
//         cout << a << " " << b << '\n';
//     }
    for (int i = 0; i < Q.size(); i++){
        if (i != Q.size() - 1 && Q[i].second != Q[i + 1].second) {
            res += Q[i].first;
        } else if (i == Q.size() - 1) {
            res += Q[i].first;
        }
        cout << res << '\n';
    }
    res += Q[Q.size() - 1].second * (m - query[n - 1].second);
    cout << res;

    return 0;
}

// 10 13 4
// 1 3
// 2 3
// 3 3
// 2 4
// 3 5
// 7 9
// 1 11
// 3 8
// 6 6
// 8 9

// r排序之后，需要寻找
// 111
//  11
//   1
//  111        1
//   111       2
//      1      2
//   111111    2
//       111   3
//        11   3
// 11111111111 1
//  这样子就是完全错误的，思路完全不可行

// 3 * 2

//   111
//  11111
//     111
//        8
//        8
//        8

代码二

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
#include<bits/stdc++.h>
using namespace std;
#define int long long
int x,y,z;
const int N=1e5+10;
const int inf=1e18;
int n,m,k;
using PII = pair<int,int>;
PII p[N];
int a[N],b[N];
signed main()
{
    cin>>n>>m>>k;
    set<int>s;
    for(int i=1;i<=n;++i)
    {
        cin>>p[i].first>>p[i].second;
        s.insert(p[i].first);
        a[i]=p[i].first,b[i]=p[i].second;
    }
    sort(p+1,p+1+n);
    sort(a+1,a+1+n);
    sort(b+1,b+1+n);
    vector<int>o;
    o.push_back(0);
    for(auto v:s)
    {
        o.push_back(v);
    }
    int lef=0,rig=0;
    int ans=0;
    multiset<int>sa;
    multiset<int>sb;
    for(int i=1;i<=n;++i)
    {
        if(i<=k)
            sa.insert(b[i]);
        else 
            sb.insert(b[i]);
    }
    
    for(int i=1;i<o.size();++i)
    {
        int L=o[i];
        //cout<<sa.size()<<" "<<sb.size()<<endl;
        while(lef<n&&p[lef+1].first<L)
        {
            lef++;
            int v=p[lef].second;
            //cout<<"e"<<p[lef].first<<" "<<p[lef].second<<endl;
            if(v>*sa.rbegin())
            {
                auto it=sb.find(v);
                sb.erase(it);
                //cout<<"a"<<endl;
            }
            else{
                if(sb.count(v)){
                    //cout<<"b"<<endl;
                    auto it=sb.find(v);
                    sb.erase(it);
                }
                else {
                    sa.erase(v);
                    if(!sb.empty()){
                        //cout<<"c"<<endl;
                        auto nxt=sb.begin();
                        sa.insert(*nxt);
                        sb.erase(nxt);
                    }
                    else{
                        //cout<<"d"<<endl;
                        cout<<ans<<endl;
                        return 0;
                    }
                }
            }
            
        }
        ans+=(m-*sa.rbegin()+1)*(L-o[i-1]);
        //cout<<L<<" "<<lef<<" "<<*sa.rbegin()<<endl;
        //cout<<ans<<endl;
    }
    cout<<ans<<endl;
    return 0;
}

D：智乃的原始部落

链接

题目描述

有这样一个经典故事，一位探险家到某个原始部落找一位向导带路。由于原式部落没有货币，所以探险家准备使用一块长度为555的金条支付这位向导555天的工资。

双方出于对对方的不信任，想到了一个方法可以避免某一方提前跑路。探险家将金条切成长度分别为1,2,21,2,21,2,2的三部分。

第一天结束后，探险家将长度为111的金条直接支付给向导。

第二天结束后，探险家将长度为222的金条支付给向导，并向他取回长度为111的金条。

第三天结束后，探险家将长度为111的金条直接支付给向导。

第四天结束后，探险家将另一块长度为222的金条支付给向导，并向他取回长度为111的金条。

第五天结束后，探险家将长度为111的金条直接支付给向导。

这样就构建了一套货币找零系统，使探险家能够在每一天的时候，“恰好”支付向导111个单位的金条。

现在有两块金条，长度分别为N,M，他准备雇佣这位向导N+M天，假设探险家切割一次长度为N的金条需要花费a的代价，切割一次长度为M的金条需要花费b的代价。

现在智乃想要知道，探险家通过切割两块金条构建货币找零系统使得他能够每一天`恰好’支付向导1个单位的金条的最小代价的具体方案，你可以给出任意一种。

输入描述:

1
2
3
第一行输入两个正整数N,M(1≤N,M≤107)表示两块金条的长度。

接下来一行输入两个整数a,b(1≤a,b≤109)，表示切割两块金条的代价分别是多少。

输出描述:

1
2
3
4
5
6
7
第一行输出三个整数ans,la,lb分别表示最小代价，第一块金条的切割次数，第二块金条的切割次数。

第二行输出一行la+1个正整数，表示切割后第一块金条每一部分的长度。

第三行输出一行lb+1个正整数，表示切割后第二块金条每一部分的长度。

你可以输出任意满足条件的方案，但是需要保证切割每一段的长度大于0，例如不能出现长度为5的金条，切2刀分成1,4，只能切1刀分成1,4两部分。

示例1

输入

复制

1
2
16 1
5 1000000000

输出

复制

1
2
3
15 3 0
2 4 8 2
1

示例2

输入

复制

1
2
1 1
1 1

输出

复制

1
2
3
0 0 0
1
1

示例3

输入

复制

1
2
10000000 10000000
1000000000 1

输出

复制

1
2
3
23 0 23
10000000
1 2 4 8 16 32 64 128 256 512 1024 2048 4096 8192 16384 32768 65536 131072 262144 524288 1048576 2097152 4194304 1611393

思路

链接

这个题我也没想明白为什么难，可能没看到数据范围，本来是想贪心，发现贪不了一点，打了暴力找了几天规律放弃了，然后把数据范围改成暴力能过的范围。本来是放到了C题的地方，然后被内测同学吐槽后改为了D题

当然，暴力也没有那么的暴力，还是需要一些贪心技巧的。

首先这个问题有一个IO方言，叫《子集mex》，感兴趣可以自行了解一下。

对于两块金条，假设长度分别为a,ba,ba,b，我们可以找零表示的最大可以表示的数字为s。我们可以用一个三元组(a,b,s)来表示一个当且状态。定义f(a,b,s)表示当前长度分别为a,b，最大可以表示的数字为s的最小代价。初始状态为f(la,lb,0)。

我们思考这样一个问题，当满足如下约束条件时

$ \left{\begin{matrix}a’\geq a\b’ \geq b \s’ \leq s \end{matrix}\right. $

必定存在f(a′,b′,s′)≤f(a,b,s)成立。所以每次dfs的时候贪心的取s准没错，除非金条剩余部分已经满足条件，需要直接加到sss中。

思考时间复杂度，发现最坏情况就是按照1,2,4,8,16,…倍增，所以最多递归log(max(n,m))次，每次dfs要么切要么切b，复杂度为O(2log(max(n,m)))=O(max(n,m)，所以暴力即可通过本题。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
#include <bits/stdc++.h>
using i64 = long long;
 
using namespace std;
const int MAXN = 1005;
const i64 INF = 1LL << 60;
i64 dp[MAXN][MAXN], c[MAXN][2], v[MAXN];  //0:'(',1:')'
bool vis[MAXN][MAXN];
i64 dp2[MAXN], dp3[MAXN];
char s[MAXN];
i64 val(int l, int r)
{
    if (l > r)
        return 0;
    if (((r - l) & 1) == 0)
        return -INF;
    if (vis[l][r])
        return dp[l][r];
    vis[l][r] = true;
    dp[l][r] = val(l + 1, r - 1) + c[l][0] + c[r][1] + (v[l] * v[r]);
    for (int i = l + 1; i < r; i += 2)
    {
        dp[l][r] = max(dp[l][r], val(l, i) + val(i + 1, r));
    }
    return dp[l][r];
}
int main()
{
    int n;
    scanf("%d",&n);
    scanf("%s",s+1);
    for (int i = 1; i <= n; ++i)
    {
        scanf("%lld",&v[i]);
    }
    for (int i = 1; i <= n; ++i)
    {
        int op = s[i] == '(';
        scanf("%lld",&c[i][op]);
        c[i][op] *= -1;
    }
    for (int i = 1; i <= n; ++i)
    {
        dp2[i] = dp3[i] = -INF;
    }
    
    for (int i = 1; i <= n; ++i)
    {
        dp2[i] = max(dp2[i], dp2[i - 1] + c[i][1]);
        for (int j = i - 1; j >= 1; j -= 2)
        {
            dp2[i] = max(dp2[i], dp2[j - 1] + val(j, i));
        }
    }
    for (int i = n; i; --i)
    {
        dp3[i] = max(dp3[i], dp3[i + 1] + c[i][0]);
        for (int j = i + 1; j <= n; j += 2)
        {
            dp3[i] = max(dp3[i], dp3[j + 1] + val(i, j));
        }
    }
    i64 ans = -INF;
    for (int i = 1; i <= n + 1; ++i)
    {
        ans = max(ans, dp2[i - 1] + dp3[i]);
    }
    printf("%lld\n",ans);
    return 0;
}