5573.叠砖块
叠砖块,第一层放一块砖,第二层放两块砖,第三层放三块砖,以此类推。
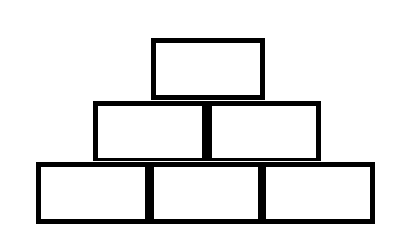
请你计算,如果要叠 n 层,则一共需要用到多少块砖。
输入格式
一个整数 n。
输出格式
一个整数,表示需要用到的砖块总数量。
数据范围
前 3 个测试点满足 1≤n≤10。
所有测试点满足 1≤n≤100。
输入样例:
输出样例:
代码
1
2
3
4
5
6
7
8
| #include <iostream>
using namespace std;
int main()
{
int n;
cin >> n;
cout << (1 + n) * n / 2;
}
|
5574.区间分组
给定 n 个整数闭区间 [l1,r1],[l2,r2],…,[ln,rn]。
请你判断能否将这 n 个区间分成两组,并使得两个组都满足:组内区间两两不重叠。
注意:
- 可以存在空组。
- [1,2] 和 [2,3] 虽然只有一个公共点,但也算作重叠。
输入格式
第一行包含整数 n。
接下来 n 行,每行包含两个整数 li,ri,。
输出格式
如果可以顺利分组,则输出 YES,否则输出 NO。
数据范围
前 66 个测试点满足 1≤n≤5。
所有测试点满足 1≤n≤2×105,0≤li<ri≤109。
输入样例1:
输出样例1:
输入样例2:
输出样例2:
输入样例3:
输出样例3:
思路
这道题目本人代码有一些冗余,还需见谅。
这道题目我的思路就是:
首先,需要将所有的区间按照区间的左端点排序。
然后进行第一次寻找,查找可以组合成一个集合的区间,同时把这些区间设置为true,表示这些区间已经在第一个集合里面。
然后第二次进行同样的查询,但是这次查询有点不一样,第一次查询如果遇到重合的情况我们是不需要处理的,但是第二次的话我们如果遇到了这种情况我们就可以直接判断这些区间无法组成两组集合了。比如说,1,2, 1,2, 3,4。这种情况我们第一个集合就会装下1,2和3,4,第二个集合就会装下1,2。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
| #include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
typedef pair<int, int> PII;
const int N = 2e5 + 10;
PII p[N];
bool st[N];
bool cmp(PII A, PII B) {
return A.first < B.first;
}
int main()
{
ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
int n;
cin >> n;
for (int i = 1; i <= n; i++) {
int l, r;
cin >> l >> r;
p[i] = {l, r};
}
sort(p + 1, p + n + 1, cmp);
int l = -1, r = -1;
for (int i = 1; i <= n; i++) {
int ll = p[i].first, rr = p[i].second;
if (ll > r) {
r = rr;
st[i] = true;
}
}
l = -1;
r = -1;
for (int i = 1; i <= n; i++) {
if (!st[i]) {
int ll = p[i].first, rr = p[i].second;
if (ll > r) {
r = rr;
st[i] = true;
} else {
cout << "NO";
return 0;
}
}
}
cout << "YES";
return 0;
}
|
5575.改变数值
原题
给定一个整数 x,初始时 x 等于 0。
有 n 个改变数值的能力,其中第 i 个能力为:将当前的 x 值增大或减少 ai。
激活第 i 个能力所需要花费的代价为 bi。
每个能力激活后均可以无限次使用。
我们的目标是通过激活一些能力,令 x 有能力变为任意整数(变化过程中可能会涉及到一些中间数)。
请你判断,该目标是否有可能实现,如果能,请你计算激活能力所需花费的最小总代价。
注意:整数分为三个部分,即正整数、零与负整数。
输入格式
第一行包含整数 n。
第二行包含 n 个整数 a1,a2,…,an。
第三行包含 n 个整数 b1,b2,…,bn。
输出格式
如果有可能实现目标,则输出激活能力所需花费的最小总代价。
否则,输出 -1。
数据范围
前 6 个测试点满足 1≤n≤10。
所有测试点满足 1≤n≤300,1≤ai≤109,1≤bi≤105。
输入样例1:
输出样例1:
输入样例2:
1
2
3
| 5
10 20 30 40 50
1 1 1 1 1
|
输出样例2:
思路
利用裴蜀定理 + 01背包问题思想来写就ok了。
任意数量的变量的线性系数组合可以凑出所有它们的 gcd的倍数。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
| #include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int N = 310;
int n;
int a[N], b[N];
map<int, int> dp;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> a[i];
}
for (int i = 1; i <= n; i++) {
cin >> b[i];
}
dp[0] = 0;
for (int i = 1; i <= n; i++) {
for (auto [x, y] : dp) {
int d = __gcd(x, a[i]);
if (dp.count(d)) {
dp[d] = min(dp[d], y + b[i]);
} else {
dp[d] = y + b[i];
}
}
}
cout << (dp[1] ? dp[1] : -1) << '\n';
return 0;
}
|
