算法练习专栏------牛客周赛 Round 41

A:小红接雨水

链接

题目描述

小红在数轴上搭起了3个宽度为1的紧挨着的矩形柱子，高度从左到右分别是a,b,ca,b,ca,b,c。小红想知道，当雨水量足够的时候，最多可以接多少单位面积的水？

输入描述:

1
2
三个正整数a,b,c，用空格隔开。
1≤a,b,c≤109

输出描述:

1
一个整数，代表可以接的雨水的最多的单位面积。

示例1

输入

复制

1
5 3 6

输出

复制

1
2

说明

1

示例2

输入

复制

1
4 7 1

输出

复制

1
0

说明

1
雨水会顺着两侧流走。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <map>
#include <unordered_map>
#include <string>
#include <cmath>
#include <set>
#include <stack>
#include <vector>
#include <deque>
#include <bitset>
#include <cstdio>
#include <iomanip>

// #define int long long
#define ull unsigned long long
#define ed '\n'
#define fi first
#define se second
#define fore(i, l, r) for(int i = (int)(l); i <=(int)r; i++)
#define debug(x) cout << "#x = " << x << ed;
#define PI acos(-1)
#define E exp(1)
#define IOS ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define me0(st) memset(st, 0, sizeof st)
#define me3f(st) memset(st, 0x3f, sizeof st)
#define pdf(x) printf("%lf", double(x))
#define pif(x) printf("%d ",  int(x))
#define scf(x) printf("%d",  int(x))
#define re return 0
#define max(a, b) ((a) > (b) ? (a) : (b))
#define min(a, b) ((a) < (b) ? (a) : (b))
#define out(x, k) cout << fixed << setprecision(k) << x << ed

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;
typedef double db;


const int INF = 1e9;
const int N = 1e5 + 10;

void solve() {
    int a, b, c;
    cin >> a >> b >> c;
    if (b < a && b < c) cout << min(a, c) - b;
    else cout << "0";
}
int main()
{
    IOS;
    int _ = 1;
    // cin >> _;
    
    while(_--) {
        solve();
    }
    
    re;
}

B:小红的排列构造

链接

题目描述

定义两个数组a和b的汉明距离为：有多少个下标iii满足ai≠bi。例如，[2,3,1]和[1,3,1]的汉明距离是1。
现在小红拿到了一个长度为n的排列p，她希望你构造一个长度为n的排列q，满足p和q的汉明距离恰好等于k。

排列指长度为n的数组，其中1到n每个元素恰好出现了一次。

输入描述:

1
2
3
4
第一行输入两个正整数n,k，代表排列p的长度，以及构造后的q和p的汉明距离。
第二行输入n个正整数pi，代表小红拿到的排列。
1≤n,k≤105
1≤ai≤n

输出描述:

1
2
如果无解，请输出-1。
否则输出n个正整数qi，代表小红构造的排列。

示例1

输入

复制

1
2
3 2
2 3 1

输出

复制

1
1 3 2

说明

1
输出[2,1,3]等排列也是合法的。

示例2

输入

复制

1
2
3 4
2 3 1

输出

复制

1
-1

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <map>
#include <unordered_map>
#include <string>
#include <cmath>
#include <set>
#include <stack>
#include <vector>
#include <deque>
#include <bitset>
#include <cstdio>
#include <iomanip>

// #define int long long
#define ull unsigned long long
#define ed '\n'
#define fi first
#define se second
#define fore(i, l, r) for(int i = (int)(l); i <=(int)r; i++)
#define debug(x) cout << "#x = " << x << ed;
#define PI acos(-1)
#define E exp(1)
#define IOS ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define me0(st) memset(st, 0, sizeof st)
#define me3f(st) memset(st, 0x3f, sizeof st)
#define pdf(x) printf("%lf", double(x))
#define pif(x) printf("%d ",  int(x))
#define scf(x) printf("%d",  int(x))
#define re return 0
#define max(a, b) ((a) > (b) ? (a) : (b))
#define min(a, b) ((a) < (b) ? (a) : (b))
#define out(x, k) cout << fixed << setprecision(k) << x << ed

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;
typedef double db;


const int INF = 1e9;
const int N = 1e5 + 10;
int a[N], b[N];
int st[N];

void solve() {
    int n, k, i, kk = 0;
    cin >> n >> k;
    fore (i, 1, n) {
        cin >> a[i];
    }
    // 注意
    if (k > n || k == 1) {
        cout << "-1";
        return;
    }

    fore (i, 1, n - k) {
        cout << a[i] << " ";
    }
    
    fore (i, n - k + 1, n) {
        if (i == n) cout << a[n - k + 1];
        else cout << a[i + 1] << " ";
    }
    
}
int main()
{
    IOS;
    int _ = 1;
    // cin >> _;
    
    while(_--) {
        solve();
    }
    
    re;
}

C:小红的循环移位

链接

题目描述

小红拿到了一个数字串，她每次操作可以使得其向左循环移动一位。
将串 s=s0s1…sn−1s = s_0s_1 . . . s_{n−1}s=s0​s1​…sn−1​ 向左循环移动一位，将得到串s1…sn−1s0s_1 . . . s_{n−1}s_0s1​…sn−1​s0​。
小红想知道，使得该数字串变成4的倍数，需要最少操作多少次？（可以包含前导零）

输入描述:

1
一个数字串，长度不超过10510^5105

输出描述:

1
2
如果无法达成目的，则输出-1。
否则输出一个整数，代表最少的操作次数。

示例1

输入

复制

1
201

输出

复制

1
1

说明

1
操作一次，数字串变成012，是4的倍数。

示例2

输入

复制

1
135

输出

复制

1
-1

说明

1
无论操作多少次，该字符串都是奇数，不可能是4的倍数。

思路

​ 思路一:就是一个纯纯的暴力,移动一次就MOD一次,这样的话就是铁铁的O(10^10)的复杂度,也就是代码一;接下来我们就要思考一下如何优化,说实话本人直接降低这O(n^2)复杂度的方法并没有想到,但是我们想到了剪枝,打个表就知道如果一个数被4整除,那么就一定需要最低位为偶数,否则直接pass,但实际上数据要是全部都是偶数就拿它没办法了,但是这样过了,所以这道题目的数据不够强.

​ 数论知识:可能很多人都没有听过这个结论:如果一个数可以被4整除,那么这个数的最后两位组成的数就一定是是4的倍数,为什么呢?请看证明:

​ 100=25x4,

我们可以知道任何一个整数都可以表示为100*a + b,因为100可以被4整除,所以是不是只要b也被4整除就可以了呀,因此可证得结论.

代码一(TLE)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <map>
#include <unordered_map>
#include <string>
#include <cmath>
#include <set>
#include <stack>
#include <vector>
#include <deque>
#include <bitset>
#include <cstdio>
#include <iomanip>

// #define int long long
#define ull unsigned long long
#define ed '\n'
#define fi first
#define se second
#define fore(i, l, r) for(int i = (int)(l); i <=(int)r; i++)
#define debug(x) cout << "#x = " << x << ed;
#define PI acos(-1)
#define E exp(1)
#define IOS ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define me0(st) memset(st, 0, sizeof st)
#define me3f(st) memset(st, 0x3f, sizeof st)
#define pdf(x) printf("%lf", double(x))
#define pif(x) printf("%d ",  int(x))
#define scf(x) printf("%d",  int(x))
#define re return 0
#define max(a, b) ((a) > (b) ? (a) : (b))
#define min(a, b) ((a) < (b) ? (a) : (b))
#define out(x, k) cout << fixed << setprecision(k) << x << ed

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;
typedef double db;a


const int INF = 1e9;
const int N = 1e5 + 10;
string s;
int len;

bool Left() {
    int k = 0;
    s = s.substr(1, len - 1) + s[0];
    while (s[k] == 0) {
        k++;
    } 
    int r = 0;
    for (int i = k; i <= len - 1; i++)
    {
        r = r * 10 + (s[i] - '0');
        r %= 4;
    }
    if (r == 0) return true;
    else return false;
}
void solve() {
    int k = 0;
    cin >> s;
    len = s.length();
    int r = 0;
    for (int i = k; i <= len - 1; i++)
    {
        r = r * 10 + (s[i] - '0');
        r %= 4;
    }
    if (!r) {
        cout << "0";
        return;
    }
    
    while (true) {
        if (Left()){
            k++;
            cout << k;
            break;
        } else k++;
        if (k > len) {
            cout << "-1";
            break;
        }
    } 
}
int main()
{
    IOS;
    int _ = 1;
    // cin >> _;
    
    while(_--) {
        solve();
    }
    
    re;
}

代码一(钻孔子过的)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <map>
#include <unordered_map>
#include <string>
#include <cmath>
#include <set>
#include <stack>
#include <vector>
#include <deque>
#include <bitset>
#include <cstdio>
#include <iomanip>

// #define int long long
#define ull unsigned long long
#define ed '\n'
#define fi first
#define se second
#define fore(i, l, r) for(int i = (int)(l); i <=(int)r; i++)
#define debug(x) cout << "#x = " << x << ed;
#define PI acos(-1)
#define E exp(1)
#define IOS ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define me0(st) memset(st, 0, sizeof st)
#define me3f(st) memset(st, 0x3f, sizeof st)
#define pdf(x) printf("%lf", double(x))
#define pif(x) printf("%d ",  int(x))
#define scf(x) printf("%d",  int(x))
#define re return 0
#define max(a, b) ((a) > (b) ? (a) : (b))
#define min(a, b) ((a) < (b) ? (a) : (b))
#define out(x, k) cout << fixed << setprecision(k) << x << ed

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;
typedef double db;


const int INF = 1e9;
const int N = 1e5 + 10;
string s;
int len;

bool Left() {
    int k = 0;
    s = s.substr(1, len - 1) + s[0];
    if (s[len - 1] % 2 == 1) return false;
    while (s[k] == 0) {
        k++;
    } 
    int r = 0;
    for (int i = k; i <= len - 1; i++)
    {
        r = r * 10 + (s[i] - '0');
        r %= 4;
    }
    if (r == 0) return true;
    else return false;
}
void solve() {
    bool flag = false;
    int k = 0;
    cin >> s;
    len = s.length();
    
    int r = 0;
    for (int i = 0; i <= len - 1; i++)
    {
        r = r * 10 + (s[i] - '0');
        r %= 4;
    }
    if (!r) {
        cout << "0";
        return;
    }
    
    while (true) {
        if (Left()){
            k++;
            cout << k;
            break;
        } else k++;
        if (k > len) {
            cout << "-1";
            break;
        }
    } 
}
int main()
{
    IOS;
    int _ = 1;
    // cin >> _;
    
    while(_--) {
        solve();
    }
    
    re;
}

代码二(加上了数论知识,直接就是O(n))

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <map>
#include <unordered_map>
#include <string>
#include <cmath>
#include <set>
#include <stack>
#include <vector>
#include <deque>
#include <bitset>
#include <cstdio>
#include <iomanip>

// #define int long long
#define ull unsigned long long
#define ed '\n'
#define fi first
#define se second
#define fore(i, l, r) for(int i = (int)(l); i <=(int)r; i++)
#define debug(x) cout << "#x = " << x << ed;
#define PI acos(-1)
#define E exp(1)
#define IOS ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define me0(st) memset(st, 0, sizeof st)
#define me3f(st) memset(st, 0x3f, sizeof st)
#define pdf(x) printf("%lf", double(x))
#define pif(x) printf("%d ",  int(x))
#define scf(x) printf("%d",  int(x))
#define re return 0
#define max(a, b) ((a) > (b) ? (a) : (b))
#define min(a, b) ((a) < (b) ? (a) : (b))
#define out(x, k) cout << fixed << setprecision(k) << x << ed

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;
typedef double db;


const int INF = 1e9;
const int N = 1e5 + 10;
char s[N];
int len, num = 0, i = 2;
void solve() {
    char a;
    while((a = getchar())!='\n')
    {
        s[i] = a;
        i++;
    }
    len = i;
    s[0] = s[i - 2];
    s[1] = s[i - 1];
    len -= 2;
//     for(int i=0;i<=len;++i) cout<<s[i];
    for(i = 1;i <= len;i++)
    {
        num = (s[i - 1] - '0') * 10 + s[i] - '0';
        if(num % 4 == 0) break;
    }
    if(i <= len) cout<< i - 1 << endl;
    else cout << -1 << endl;
}
int main()
{
    IOS;
    int _ = 1;
    // cin >> _;
    
    while(_--) {
        solve();
    }
    
    re;
}

D:小红的好串

链接

题目描述

小红定义一个字符串是“好串”，当且仅当该该字符串在长度和它相等的字符串中，”red”子序列的数量是最多的。
例如，”rreedd”是好串，因为包含了8个”red”子序列。而”redred”则不是好串。

现在小红拿到了一个字符串，她有多次询问，每次询问一个区间，你需要回答将该区间对应的子串修改为好串的最小修改次数（每次修改可以修改任意一个字符）。

输入描述:

1
2
3
4
5
第一行输入两个正整数n,q，代表字符串的长度和询问次数。
第二行输入一个长度为n的、仅由小写字母组成的字符串。
接下来的q行，每行输入两个正整数l,r，代表询问的是第l个字符到第r个字符组成的子串。
1≤n,q≤105
1≤l≤r≤n

输出描述:

1
输出q行，每行输出一个整数，代表将该字符串修改为好串的最小修改次数。

示例1

输入

复制

1
2
3
4
5
8 3
rreeddrr
1 4
1 6
3 8

输出

复制

1
2
3
1
0
6

说明

1
2
3
第一次询问的子串是"rree"，修改为"rred"即可，只需要修改1个字符。
第二次询问的子串是"rreedd"，本身即为好串，不需要修改。
第三次询问的子串是"eeddrr"，修改为"rreedd"需要修改6次。

思路

​ 思路:我们将r看作0,e看作1,d看作2,我们用一个数组sum[i] [j]存前i个数里j对应字母的个数.随后在查询l~r之间需要修改的次数的时候我们就可以分四类讨论,第一种是r - l + 1 < 3的时候直接输出0即可.再一种是(r - l + 1) % 3 == 0的,这种情况也很好处理,直接输出三部分分别和r,e,d字母对应需要的个数的差的个数即可,这样讲可能有点绕,也就是比如6,你本来应该需要rreedd这样的序列,但是给出的是reeeed,这种情况就是第1段不对,应该修改为2,修改字母的数量也就是(2-1) + (2 - 2) + (2 - 1) = 2了,这样应该就满清楚了吧.

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <map>
#include <unordered_map>
#include <string>
#include <cmath>
#include <set>
#include <stack>
#include <vector>
#include <deque>
#include <bitset>
#include <cstdio>
#include <iomanip>

// #define int long long
#define ull unsigned long long
#define ed '\n'
#define fi first
#define se second
#define fore(i, l, r) for(int i = (int)(l); i <=(int)r; i++)
#define debug(x) cout << "#x = " << x << ed;
#define PI acos(-1)
#define E exp(1)
#define IOS ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define me0(st) memset(st, 0, sizeof st)
#define me3f(st) memset(st, 0x3f, sizeof st)
#define pdf(x) printf("%lf", double(x))
#define pif(x) printf("%d ",  int(x))
#define scf(x) printf("%d",  int(x))
#define re return 0
// #define max(a, b) ((a) > (b) ? (a) : (b))
// #define min(a, b) ((a) < (b) ? (a) : (b))
#define out(x, k) cout << fixed << setprecision(k) << x << ed

using namespace std;

// typedef pair<int, int> PII;
// typedef long long LL;
// typedef double db;


const int INF = 1e9;
const int N = 1e5+10;
int sum[N][3],a[N];
char s[N];

int get(int l,int r,int x,int y,int z)
{
	return x-(sum[l+x-1][0]-sum[l-1][0])+y-(sum[l+x+y-1][1]-sum[l+x-1][1])+z-(sum[r][2]-sum[l+x+y-1][2]);
}

void solve() {
	int n;
    cin >> n;
	int q;
    cin >> q;
	scanf("%s", s + 1);
	fore (i, 1, n)
	    if(s[i] == 'r') a[i] = 0;
	    else if(s[i] =='e') a[i]=1;
	    else a[i] = 2;
	
	fore (i, 1, n)
	{
		sum[i][0] = sum[i - 1][0];
		sum[i][1] = sum[i - 1][1];
		sum[i][2] = sum[i - 1][2];
		sum[i][a[i]] ++;
	}
	
	while(q--)
	{
		int l,r;
        cin >> l >> r;
		int len = r - l + 1,cnt = len / 3;
		if(len < 3)
		{
			cout << 0 << ed;
			continue;
		}
		if(len % 3 == 0)
		  cout << get(l, r, cnt, cnt, cnt) << ed;
		else if(len % 3 == 1)
		  cout << min({get(l, r, cnt+1, cnt, cnt),get(l, r, cnt, cnt + 1, cnt),get(l,r, cnt, cnt, cnt + 1)}) << ed; 
		else
		  cout << min({get(l, r, cnt+1, cnt+1, cnt),get(l, r, cnt + 1, cnt,cnt + 1),get(l, r, cnt,cnt + 1,cnt + 1)}) << ed;
	}
     
}
int main()
{
    

    int _ = 1;
    // cin >> _;
    
    while(_--) {
        solve();
    }
    
    return 0;
}



E/F:小红的树上赋值(困难)

链接

题目描述

本题为easy版本，和hard版本的唯一区别是l和r的值是固定的！

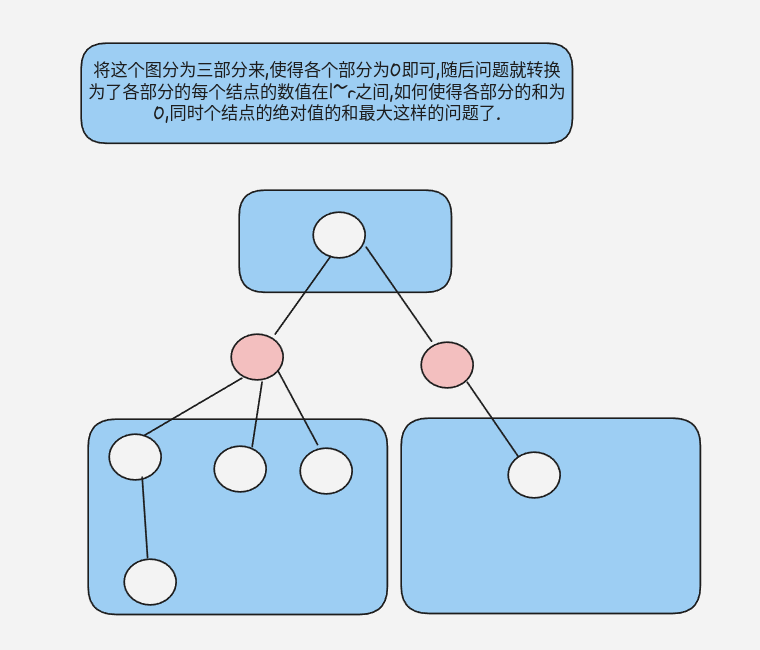
小红拿到了一棵有根树，根节点为1号节点，其中一些节点被染成了红色。她希望你给每个节点都赋一个权值（权值在[l,r]区间内），满足所有红点的子树权值和为0。
小红希望最终所有节点的绝对值之和尽可能大，你能帮小红给出一个赋值方案吗？

输入描述:

1
2
3
4
5
6
第一行输入三个整数n,l,r，代表树的节点数量，以及每个节点权值的区间。
第二行输入一个长度为nnn的字符串，代表每个节点的染色情况。第i个字符为'R'代表i号节点被染成红色，'W'代表未被染色。
接下来的n−1行，每行输入2个正整数u,v，代表节点u和节点v有一条边连接。
1≤n≤105
1≤u,v≤n
l=−1,r=1

输出描述:

1
一行输出n个整数，代表每个节点的赋值情况。如果有多种合法的树都能达成绝对值之和最大，给出任意一个方案即可。

示例1

输入

复制

1
2
3
4
3 -1 1
RWR
1 2
1 3

输出

复制

1
-1 1 0

思路

​ 这道题目分析别人代码老半天,最后得知其中的思路原来是这样,只能说是秒啊秒啊.首先说一下构造.首先是基本的加边,构成一颗数值后按照下面的思路走即可.

image-20240505233958511

然后我们可以稍微观察一下这个问题其实又转换为了:有?,r,r,r… l, ?, r, r, …. l, l, ?, r, r…. 这些序列,现在需要求出其中和为0,绝对值和最大数值,然后我们打标可以发现**(不打表,自己稍微思考一下也可以知道的)**:

l=-1,r=2,设n=6

-1,-7, 2, 2, 2, 2

-1, -1,-4, 2, 2, 2

-1, -1, -1, -1,2, 2

随着绝对值小的数的增多,那么绝对值的和肯定也会减少,那么我们就需要即使止损,尽可能让绝对值少的少一些就可以了,这样只需要等到绝对值少的和绝对值大二者的和第一次相同或者前者大于后者即可求出最佳答案了.

这样的讲解可能不是很明白,但是语言方面的表述只能到这里了,如有疑问请联系我898561494.

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
#include<bits/stdc++.h>
using namespace std;
inline int read()
{
    int x=0;char ch=getchar();
    while(!isdigit(ch)) ch=getchar();
    while(isdigit(ch)) x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
    return x;
}
int stk[10],tp;
inline void write(int x)
{
    if(!x) return puts("0"),void();
    tp=0;
    while(x) stk[++tp]=x%10,x/=10;
    while(tp) putchar(stk[tp--]^48);
    putchar('\n');
}
const int N=1e5+10,M=2e5+10;
int n,l,r,ans[N],gr[N],num[N];
int first[N],to[M],nxt[M],cnt;
char a[N];
vector<int>S[N];
inline void inc(int x,int y) {nxt[++cnt]=first[x],to[cnt]=y,first[x]=cnt;}
 
// 
void dfs(int x,int fr)
{
    if(a[x]=='R') gr[x]=x;
    else gr[x]=gr[fr];
    num[x] = 1;
    for(int i=first[x],v;i;i=nxt[i])
    {
        if((v=to[i])==fr) continue;
        dfs(v,x);
        if(a[v]!='R') num[x]+=num[v];
    }
}
int main()
{
    scanf("%d%d%d%s",&n,&l,&r,a+1);
    // 1.基本的加边操作
    for(int i=1,u,v;i<n;i++)
        scanf("%d%d",&u,&v),inc(u,v),inc(v,u);
    // 2.dfs
    dfs(1,0);
    for(int i=1;i<=n;i++) S[gr[i]].push_back(i);
    for(int x:S[0]) ans[x]=abs(l)>abs(r)?l:r;
    for(int i=1;i<=n;i++)
        if(a[i]=='R')
        {
            // for(int x:S[i]) cerr<<x<<" ";
            // cerr<<endl;
            // if(num[i]==1) continue;
            for(int j=1;j<=num[i];j++)
            {
                if(1ll*min(abs(l),abs(r))*j>=1ll*max(abs(l),abs(r))*(num[i]-j))
                {
                    // cerr<<j<<endl;
                    long long sum=0;
                    for(int k=0;k<j-1;k++) ans[S[i][k]]=abs(l)>abs(r)?r:l,sum+=ans[S[i][k]];
                    for(int k=j;k<num[i];k++) ans[S[i][k]]=abs(l)>abs(r)?l:r,sum+=ans[S[i][k]];
                    ans[S[i][j-1]]=-sum;
                    break;
                }
            }
        }
    for(int i=1;i<=n;i++)
        printf("%d%c",ans[i]," \n"[i==n]);
	return 0;
}