A:「QFOI R2」水落溪流浅浅 题目描述 小 R 是一个可爱的女孩子,某天晚上 $23$ 点她在提交作业时,发现截止时间是当天凌晨 $0$ 点。为了避免悲剧再次发生,她向你介绍“$30$ 小时制”。
$30$ 小时制的一天长度依然为 $24$ 小时,只是每天的时间范围从 $00:00\sim 23:59$ 变成了 $06:00\sim 29:59$。其中,对于 $24$ 小时制下在 $06:00\sim 23:59$ 之间的时间,其表示方式不变,而到了次日 $00:00$ 以后,保持日期不变,时间的小时部分继续增加,直到到达次日 $06:00$。
例如,下表是一些时间的对应关系:
$24$ 小时制
$30$ 小时制
$2024$ 年 $2$ 月 $13$ 日 $06:00$
$2024$ 年 $2$ 月 $13$ 日 $06:00$
$2024$ 年 $2$ 月 $13$ 日 $12:00$
$2024$ 年 $2$ 月 $13$ 日 $12:00$
$2024$ 年 $2$ 月 $13$ 日 $18:00$
$2024$ 年 $2$ 月 $13$ 日 $18:00$
$2024$ 年 $2$ 月 $14$ 日 $00:00$
$2024$ 年 $2$ 月 $13$ 日 $24:00$
$2024$ 年 $2$ 月 $14$ 日 $05:59$
$2024$ 年 $2$ 月 $13$ 日 $29:59$
$2024$ 年 $2$ 月 $14$ 日 $06:00$
$2024$ 年 $2$ 月 $14$ 日 $06:00$
现给定一个 $24$ 小时制时间,请将其转化为 $30$ 小时制。
由于小 R 也认为闰年处理很烦,因此你不需要告诉她日期,只需要告诉她时间即可。
输入格式 一行一个字符串,格式为 hh:mm,表示一个 $24$ 小时制时间。特别地,若小时和分钟不足两位数,会补前导零至两位。
输出格式 一行一个字符串,格式为 hh:mm,表示对应的 $30$ 小时制时间。若小时和分钟不足两位数,你同样需要补前导零至两位。你不需要考虑日期是否变化。
样例 #1 样例输入 #1 样例输出 #1 样例 #2 样例输入 #2 样例输出 #2 样例 #3 样例输入 #3 样例输出 #3 提示 样例 $1$ 解释
$14:00$ 属于 $06:00\sim 23:59$ 的范围,因此表示方式不变。
数据范围
本题不采用捆绑测试。
对于全部数据:保证输入为【输入格式】中约定合法的 $24$ 小时制时间。
提示
【题目描述】部分的表格提供了更多可供使用的样例。
代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 #include <iostream> #include <cstring> #include <algorithm> #include <queue> #include <map> #include <unordered_map> #include <string> #include <cmath> #include <set> #include <stack> #include <vector> #include <deque> #include <bitset> #include <cstdio> #define ull unsigned long long #define ed '\n' #define fi first #define se second #define fore(i, l, r) for(int i = (int)(l); i <=(int)r; i++) #define debug(x) cout << "#x = " << x << ed; #define PI acos(-1) #define E exp(1) #define IOS ios::sync_with_stdio(false),cin.tie(0),cout.tie(0); #define me0(st) memset(st, 0, sizeof st) #define me3f(st) memset(st, 0x3f, sizeof st) #define pdf(x) printf("%lf" , double(x)) #define pif(x) printf("%d " , int(x)) #define scf(x) printf("%d" , int(x)) #define re return #define max(a, b) ((a) > (b) ? (a) : (b)) #define min(a, b) ((a) < (b) ? (a) : (b)) using namespace std;typedef pair<int , int > PII;typedef long long LL;typedef double db;const int INF = 1e9 ;const int N = 2e5 + 10 ;void solve () int h, m;if (s[0 ] == '0' ) h = s[1 ] - '0' ;else h = (s[0 ] - '0' ) * 10 + s[1 ] - '0' ;if (h >= 5 && h <= 23 ) cout << s;else cout << h + 24 << ":" << s[3 ] << s[4 ];int main () int _ = 1 ;while (_--) {solve ();0 ;
B:U420200 「QFOI R2」寺秋山霭苍苍 「QFOI R2」寺秋山霭苍苍 题目背景 本题可能用到的公式:
两点间的距离公式:$(x_1,y_1),(x_2,y_2)$ 之间的距离为 $\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}$。
海伦公式:若三角形三边长为 $a,b,c$,设半周长 $p=\frac{a+b+c}{2}$,则三角形面积为 $S=\sqrt{p(p-a)(p-b)(p-c)}$。
题目描述 小 R 是一个可爱的女孩子,她的几何太差了,于是她向你求助这道几何题。
在平面直角坐标系中,有一个 $\triangle\textrm{ABC}$,其顶点坐标为 $\textrm{A}(x_1,y_1),\textrm{B}(x_2,y_2),\textrm{C}(x_3,y_3)$。
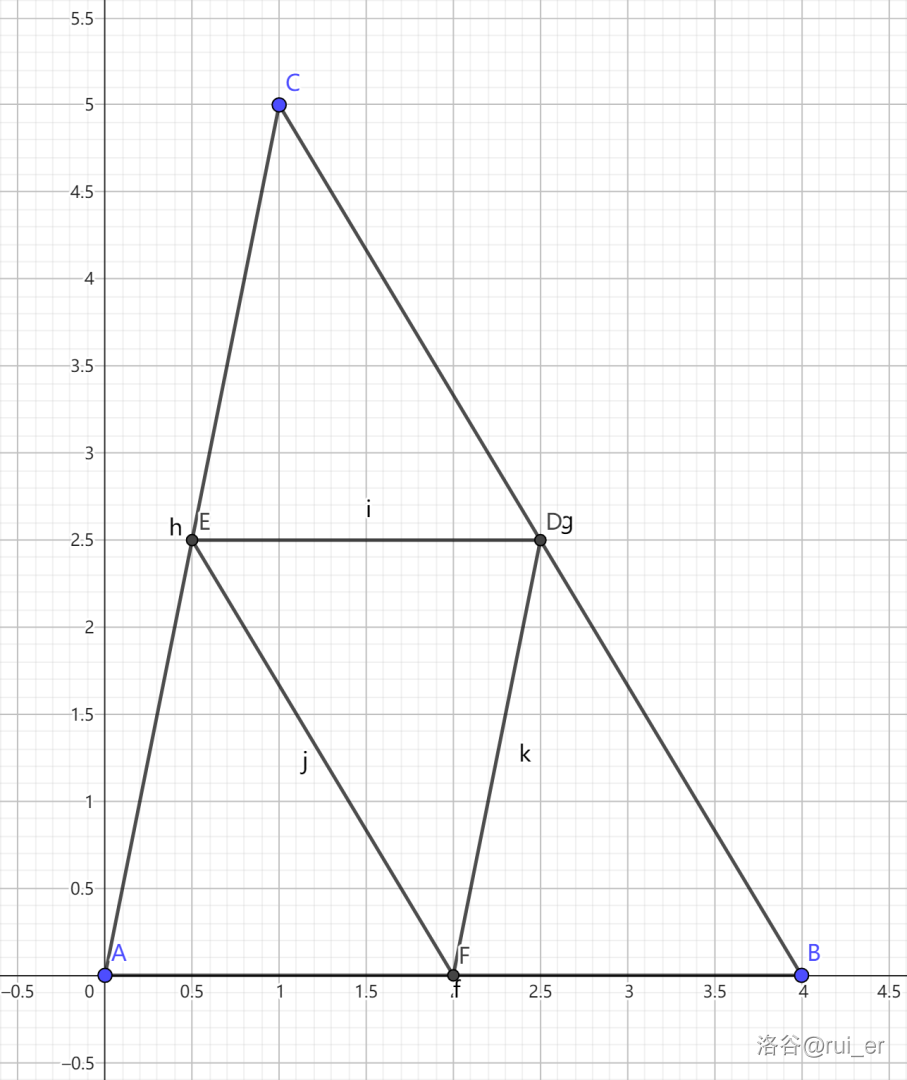
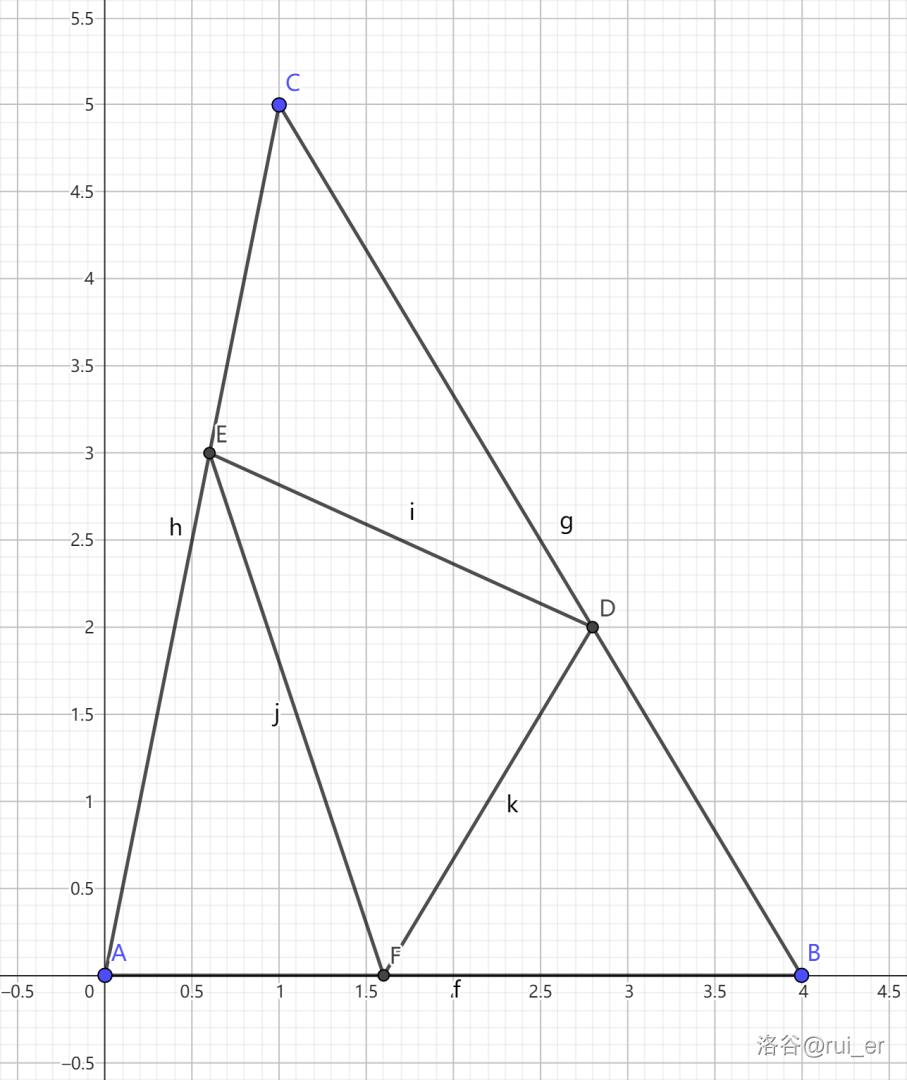
对于实数 $p\in(0,1)$,在 $\textrm{BC},\textrm{CA},\textrm{AB}$ 边上分别取点 $\textrm{D},\textrm{E},\textrm{F}$,使得 $\frac{|\textrm{AF}|}{|\textrm{AB}|}=\frac{|\textrm{BD}|}{|\textrm{BC}|}=\frac{|\textrm{CE}|}{|\textrm{CA}|}=p$,则称 $\triangle\textrm{DEF}$ 为 $\triangle\textrm{ABC}$ 的“$p$ 比例三角形”。
请在 $[l,r]$ 范围内选择实数 $p$,使得 $\triangle\textrm{ABC}$ 的“$p$ 比例三角形”的面积最小。你需要求出这个面积。
输入格式 一行八个实数 $l,r,x_1,y_1,x_2,y_2,x_3,y_3$。
输出格式 一行一个实数 $S_{\min}$,表示最小面积。
你的输出被认为是正确的,当且仅当其与标准答案的绝对或相对误差不超过 $10^{-4}$。
样例 #1 样例输入 #1 1 0 .40 0 .60 0 .00 0 .00 4 .00 0 .00 1 .00 5 .00
样例输出 #1 样例 #2 样例输入 #2 1 0 .20 0 .40 0 .00 0 .00 4 .00 0 .00 1 .00 5 .00
样例输出 #2 提示 样例 $1$ 解释
可以证明,当 $p=0.5$ 时面积最小,为 $2.5$。
样例 $2$ 解释
可以证明,当 $p=0.4$ 时面积最小,为 $2.8$。
评分方式
本题采用自定义校验器(Special Judge)进行评测。
你的输出被认为是正确的,当且仅当其与标准答案的绝对或相对误差不超过 $10^{-4}$。
数据范围
本题采用捆绑测试。只有通过子任务中所有测试点以及所有依赖的子任务,才能获得相应的分数。
对于全部数据:$0 < l < r < 1$,$0\le x_1,y_1,x_2,y_2,x_3,y_3\le 10^5$,保证输入构成三角形,所有实数的小数点后位数不超过 $2$。
子任务一($20$ 分):$l=0.10,r=0.90$。
子任务二($20$ 分):$x_1=y_1=y_2=x_3=0.00$。
子任务三($20$ 分):$x_1=y_1=y_2=0.00$。依赖子任务二。
子任务四($40$ 分):无特殊限制。依赖子任务一、二、三。
提示
本题可能用到的公式:
两点间的距离公式:$(x_1,y_1),(x_2,y_2)$ 之间的距离为 $\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}$。
海伦公式:若三角形三边长为 $a,b,c$,设半周长 $p=\frac{a+b+c}{2}$,则三角形面积为 $S=\sqrt{p(p-a)(p-b)(p-c)}$。
思路
思路一:
代码一(纯数学推导,初中知识) 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 #include <iostream> #include <cstring> #include <algorithm> #include <queue> #include <map> #include <unordered_map> #include <string> #include <cmath> #include <set> #include <stack> #include <vector> #include <deque> #include <bitset> #include <cstdio> #include <bits/stdc++.h> #include <iomanip> #define ull unsigned long long #define ed '\n' #define fi first #define se second #define fore(i, l, r) for(int i = (int)(l); i <=(int)r; i++) #define debug(x) cout << "#x = " << x << ed; #define PI acos(-1) #define E exp(1) #define IOS ios::sync_with_stdio(false),cin.tie(0),cout.tie(0); #define me0(st) memset(st, 0, sizeof st) #define me3f(st) memset(st, 0x3f, sizeof st) #define pdf(x) printf("%lf" , double(x)) #define pif(x) printf("%d " , int(x)) #define scf(x) printf("%d" , int(x)) #define re return 0 #define max(a, b) ((a) > (b) ? (a) : (b)) #define min(a, b) ((a) < (b) ? (a) : (b)) #define out(x, k) cout << fixed << setprecision(k) << x << ed using namespace std;typedef pair<int , int > PII;typedef long long LL;typedef double db;const int INF = 1e9 ;const int N = 1e5 + 10 ;inline double calc (double S, double p) return S - 3.0 * (S * p * (1.0 - p));void solve () double l, r, x1, y1, x2, y2, x3, y3;double a = sqrt ((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2));double b = sqrt ((x1 - x3) * (x1 - x3) + (y1 - y3) * (y1 - y3));double c = sqrt ((x2 - x3) * (x2 - x3) + (y2 - y3) * (y2 - y3));double p = (a + b + c) * 0.5 ;double S = sqrt (p * (p - a) * (p - b) * (p - c));double k = 0.5 ;min (k, r);max (k, l);out (calc (S, k), 12 );int main () int _ = 1 ;while (_--) {solve ();
代码二 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 #include <bits/stdc++.h> double distance (double x1, double y1, double x2, double y2) return std::sqrt ((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2));double triangle_area (double a, double b, double c) double p = (a + b + c) / 2 ;return std::sqrt (p * (p - a) * (p - b) * (p - c));double calculateNewPointX (double x1, double x2, double p) return x1 + p * (x2 - x1);double calculateNewPointY (double y1, double y2, double p) return y1 + p * (y2 - y1);double find_min_area (double l, double r, double x1, double y1, double x2, double y2, double x3, double y3) double t = distance (x1, y1, x2, y2);double k = distance (x2, y2, x3, y3);double o = distance (x3, y3, x1, y1);double min_area = triangle_area (t,k,o); double best_p = 0.0 ; for (double p = l; p <= r; p += 0.0001 )double xD = calculateNewPointX (x1, x2, p);double yD = calculateNewPointY (y1, y2, p);double xE = calculateNewPointX (x2, x3, p);double yE = calculateNewPointY (y2, y3, p);double xF = calculateNewPointX (x3, x1, p);double yF = calculateNewPointY (y3, y1, p);double a = distance (xD, yD, xE, yE);double b = distance (xE, yE, xF, yF);double c = distance (xF, yF, xD, yD);double area = triangle_area (a, b, c);if (area < min_area)return min_area;int main () double l, r, x1, y1, x2, y2, x3, y3;double min_area = find_min_area (l, r, x1, y1, x2, y2, x3, y3);printf ("%.12lf" ,min_area);return 0 ;
C:U420201 「QFOI R2」树色尤含残雨 「QFOI R2」树色尤含残雨 题目描述 小 R 是一个可爱的女孩子,她喜欢分解质因数。
她有一个正整数 $x$。每次操作可以选择 $p_1,\alpha_1,p_2,\alpha_2$ 满足 $p_1,p_2$ 为两不同质数且 $\alpha_1,\alpha_2$ 为正整数,若 $x$ 是 $p_1^{\alpha_1}p_2^{\alpha_2}$ 的整数倍,就将 $x$ 除以 $p_1^{\alpha_1}p_2^{\alpha_2}$,否则操作无效。
请你求出通过若干次操作可以得到的最小的 $x$。
输入格式 一行一个整数 $x$。
输出格式 一个整数,表示可以得到的最小的 $x$。
样例 #1 样例输入 #1 样例输出 #1 样例 #2 样例输入 #2 样例输出 #2 样例 #3 样例输入 #3 样例输出 #3 提示 样例 $1$ 解释
无法进行任何有效操作。
样例 $2$ 解释
可以进行以下两次操作:
令 $p_1=2,\alpha_1=1,p_2=3,\alpha_2=1$,将 $x$ 除以 $p_1^{\alpha_1}p_2^{\alpha_2}=2^13^1=6$,得到 $x=20$。
令 $p_1=2,\alpha_1=2,p_2=5,\alpha_2=1$,将 $x$ 除以 $p_1^{\alpha_1}p_2^{\alpha_2}=2^25^1=20$,得到 $x=1$。
数据范围
本题采用捆绑测试。只有通过子任务中所有测试点以及所有依赖的子任务,才能获得相应的分数。
对于全部数据:$2\le x\le 10^9$。
子任务一($10$ 分):$x\le 10$。
子任务二($20$ 分):$x$ 为“无平方因子数”$^\dagger$。
子任务三($20$ 分):$x$ 为一个质数的正整数次幂。
子任务四($20$ 分):$x\le 10^5$。依赖子任务一。
子任务五($30$ 分):无特殊限制。依赖子任务一、二、三、四。
$\dagger$ 称一个数 $x$ 为“无平方因子数”,当且仅当不存在大于一的整数 $k$,使得 $x$ 是 $k^2$ 的整数倍。
思路
这道题目我乍眼一看,哦?so easy,不就是特判类型题目吗,然后直接一发WA。
然后仔细分析(实际这道题目我就是打表打出来的): 通过打表我们可以发现这样的规律:
对于质数来说,直接输出本身即可
对于一般数来说,如果分解出的质因子的类型数量为偶数,就一定可以最后变成0;如果是是奇数(由于不是质数所以 > 1) ,那么我们只需要查看一下是否存在指数超过1的即可,如果存在则输出第一小的质因子就OK了,反之则输出1。
代码一(本人:思维分析) 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 #include <iostream> #include <cstring> #include <algorithm> #include <queue> #include <map> #include <unordered_map> #include <string> #include <cmath> #include <set> #include <stack> #include <vector> #include <deque> #include <bitset> #include <cstdio> #define ull unsigned long long #define ed '\n' #define fi first #define se second #define fore(i, l, r) for(int i = (int)(l); i <=(int)r; i++) #define debug(x) cout << "#x = " << x << ed; #define PI acos(-1) #define E exp(1) #define IOS ios::sync_with_stdio(false),cin.tie(0),cout.tie(0); #define me0(st) memset(st, 0, sizeof st) #define me3f(st) memset(st, 0x3f, sizeof st) #define pdf(x) printf("%lf" , double(x)) #define pif(x) printf("%d " , int(x)) #define scf(x) printf("%d" , int(x)) #define scfd(x) printf("%lf" , double(x)) #define re return #define max(a, b) ((a) > (b) ? (a) : (b)) #define min(a, b) ((a) < (b) ? (a) : (b)) using namespace std;typedef pair<int , int > PII;typedef long long LL;typedef double db;const int INF = 1e9 ;const int N = 2e5 + 10 ;int , int > st;long long res, ans;void solve () int n, k;int nn = n;bool flag = false ;for (int i = 2 ; i * i <= n; i++) {if (n % i == 0 ) {if (!flag) {true ;else continue ;int kk = 0 ;while (n % i == 0 ) {max (ans, kk);if (n == 1 ) break ;if (n > 1 ) {if (res == 1 ) {return ;if (res % 2 == 0 ) cout << "1" ;else {if (ans > 1 ) cout << "1" ;else {int main () int _ = 1 ;while (_--) {solve ();0 ;
D:「QFOI R2」钟声远带斜阳 原题
题目描述 注意:本题中的所有数列下标从 $0$ 开始。
小 R 是一个可爱的女孩子,她喜欢研究无穷数列。
她称一个无穷数列 $b$ 是美妙的,当且仅当存在自然数 $k_0$,使得对于所有 $k\ge k_0$,都满足 $b$ 中下标在区间 $[k_0,k]$ 内的所有数的和非负(即 $\sum_{i=k_0}^kb_i\ge 0$)。例如,数列 $\alpha_i=i-5$ 是美妙的,取 $k_0=5$ 符合要求;但 $\beta_i=-i$ 不是美妙的。
她目前只有一个长度为 $n$ 的有穷数列 $a$,可以进行任意次以下三种操作:
花费 $p$ 的代价,选择一个整数 $i$($0\le i < n$),将 $a_i$ 增加一。
花费 $q$ 的代价,选择一个整数 $i$($0\le i < n$),将 $a_i$ 删除,同时更新 $n$ 为新的数列长度。不能将数列删空。
花费 $r$ 的代价,选择两个整数 $i,j$($0\le i < j < n$),交换 $a_i$ 与 $a_j$。
她希望在若干次操作后,用无限个有穷数列 $a$ 依次相接得到无穷数列 $b$(即 $b_i=a_{i\bmod n}$),使得 $b$ 是美妙的。请你求出最小的代价。
输入格式 第一行四个整数 $n,p,q,r$。
第二行 $n$ 个整数,表示数列 $a$。
输出格式 一行,一个整数,表示最小代价。
样例 #1 样例输入 #1 样例输出 #1 样例 #2 样例输入 #2 样例输出 #2 样例 #3 样例输入 #3 样例输出 #3 提示 样例 $1$ 解释
花费 $p=1$ 的代价将 $a_3$ 增加一,得到数列 $b=[2,-2,3,-2,-1,2,-2,3,-2,-1,\cdots]$ 是美妙的,取 $k_0=2$ 符合要求。
可以证明不存在代价更小的方案。
样例 $2$ 解释
花费 $q=1$ 的代价将 $a_1$ 删除,得到数列 $b=[2,3,-3,-1,2,3,-3,-1,\cdots]$ 是美妙的,取 $k_0=0$ 符合要求。
可以证明不存在代价更小的方案。
数据范围
本题采用捆绑测试。只有通过子任务中所有测试点以及所有依赖的子任务,才能获得相应的分数。
对于全部数据:$1\le n\le 10^5$,$1\le p,q,r\le 10^9$,$|a_i|\le 10^9$。
子任务一($10$ 分):$n=1$。
子任务二($10$ 分):$n\le 10$。依赖子任务一。
子任务三($20$ 分):$|a_i|\le 1$。
子任务四($20$ 分):$\sum|a_i|\le 10^5$。依赖子任务三。
子任务五($40$ 分):无特殊限制。依赖子任务一、二、三、四。
思路
贪心 + 前缀和,具体思路略……
代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 #include <bits/stdc++.h> using namespace std;const int N = 100100 ;typedef long long ll;int main () scanf ("%lld%lld%lld%lld" ,&n,&p,&q,&r);for (int i=1 ;i<=n;i++)scanf ("%lld" ,&a[i]),b[i]=a[i],su+=a[i];sort (b+1 ,b+n+1 );if (su>=0 ){printf ("0" );return 0 ;0 -su;0 ;for (int i=1 ;i<n;i++){if (sum<0 && b[i]<0 ) h2+=min (min (-b[i],-sum)*p,q),sum+=-b[i];if (sum>=0 ) break ;if (sum<0 ) h2+=(0 -sum)*p;printf ("%lld" ,h2);return 0 ;