算法练习专栏——Codeforces——Codeforces Round944 (Div. 4)

C. Clock and Strings

There is a clock labeled with the numbers $1$ through $12$ in clockwise order, as shown below.

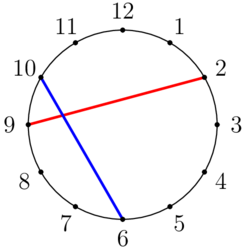
In this example, $(a,b,c,d)=(2,9,10,6)$, and the strings intersect.

Alice and Bob have four distinct integers $a$, $b$, $c$, $d$ not more than $12$. Alice ties a red string connecting $a$ and $b$, and Bob ties a blue string connecting $c$ and $d$. Do the strings intersect? (The strings are straight line segments.)

Input

The first line contains a single integer $t$ ($1 \leq t \leq 5940$) — the number of test cases.

The only line of each test case contains four distinct integers $a$, $b$, $c$, $d$ ($1 \leq a, b, c, d \leq 12$).

Output

For each test case, output “YES” (without quotes) if the strings intersect, and “NO” (without quotes) otherwise.

You can output “YES” and “NO” in any case (for example, strings “yEs”, “yes”, and “Yes” will be recognized as a positive response).

Example

input

15
2 9 10 6
3 8 9 1
1 2 3 4
5 3 4 12
1 8 2 10
3 12 11 8
9 10 12 1
12 1 10 2
3 12 6 9
1 9 8 4
6 7 9 12
7 12 9 6
10 12 11 1
3 9 6 12
1 4 3 5

output

YES
NO
NO
YES
YES
NO
NO
NO
NO
NO
NO
YES
YES
YES
YES

Note

The first test case is pictured in the statement.

In the second test case, the strings do not intersect, as shown below.

翻译

有一个时钟，按顺时针顺序标有数字 $1$ 到 $12$ ，如下所示。

在此示例中， $(a,b,c,d)=(2,9,10,6)$ 和字符串相交。

Alice 和 Bob 有四个不同的整数 $a$ 、 $b$ 、 $c$ 、 $d$ 不超过 $12$ 。 Alice 系一根红色绳子连接 $a$ 和 $b$ ，Bob 系一根蓝色绳子连接 $c$ 和 $d$ 。字符串相交吗？ (弦是直线段。)

输入

第一行包含一个整数 $t$ ( $1 \leq t \leq 5940$ ) - 测试用例的数量。

每个测试用例的唯一行包含四个 不同 整数 $a$ 、 $b$ 、 $c$ 、 $d$ ( $1 \leq a, b, c, d \leq 12$ )。

输出

对于每个测试用例，如果字符串相交，则输出“YES”（不带引号），否则输出“NO”（不带引号）。

您可以在任何情况下输出“YES”和“NO”（例如，字符串“yEs”、“yes”和“Yes”将被识别为肯定响应）。

Example

input

15
2 9 10 6
3 8 9 1
1 2 3 4
5 3 4 12
1 8 2 10
3 12 11 8
9 10 12 1
12 1 10 2
3 12 6 9
1 9 8 4
6 7 9 12
7 12 9 6
10 12 11 1
3 9 6 12
1 4 3 5

output

YES
NO
NO
YES
YES
NO
NO
NO
NO
NO
NO
YES
YES
YES
YES

笔记

第一个测试用例如声明中所示。

在第二个测试用例中，字符串不相交，如下所示。

思路

​ 基本思路就是直接看第二条线的两个点的位置是否在第一条线的异侧即可判断是否相交.

代码

#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <map>
#include <unordered_map>
#include <string>
#include <cmath>
#include <set>
#include <stack>
#include <vector>
#include <deque>
#include <bitset>
#include <cstdio>
#include <iomanip>

// #define int long long
#define ull unsigned long long
#define ed '\n'
#define fi first
#define se second
#define fore(i, l, r) for(int i = (int)(l); i <=(int)r; i++)
#define debug(x) cout << "#x = " << x << ed;
#define PI acos(-1)
#define E exp(1)
#define IOS ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define me0(st) memset(st, 0, sizeof st)
#define me3f(st) memset(st, 0x3f, sizeof st)
#define pdf(x) printf("%lf", double(x))
#define pif(x) printf("%d ",  int(x))
#define scf(x) printf("%d",  int(x))
#define re return 0
#define max(a, b) ((a) > (b) ? (a) : (b))
#define min(a, b) ((a) < (b) ? (a) : (b))
#define out(x, k) cout << fixed << setprecision(k) << x << ed

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;
typedef double db;


const int INF = 1e9;
const int N = 1e5 + 10;
const LL mod = 998244353;


void solve(){
    int a, b, c, d;
    cin >> a >> b >> c >> d; 
    int min1 = min(a, b), min2 = min(c, d), max1 = max(a, b), max2 = max(a, b);

    if ((c >= min1 && c <= max1) && !(d >= min1 && d <= max1)) cout << "YES\n";
    else cout << "NO\n"; 

    
}
int main()
{
    IOS;
    int _ = 1;
    cin >> _;
    
    while(_--) {
        solve();
    }
    
    re;
}

D. Binary Cut

You are given a binary string$^{\dagger}$. Please find the minimum number of pieces you need to cut it into, so that the resulting pieces can be rearranged into a sorted binary string.

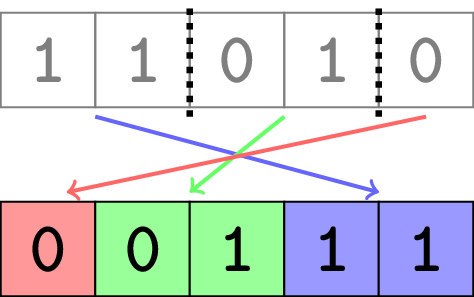
Note that:

• each character must lie in exactly one of the pieces;
• the pieces must be contiguous substrings of the original string;
• you must use all the pieces in the rearrangement.

$^{\dagger}$ A binary string is a string consisting of characters $\texttt{0}$ and $\texttt{1}$. A sorted binary string is a binary string such that all characters $\texttt{0}$ come before all characters $\texttt{1}$.Input

The first line contains a single integer $t$ ($1 \leq t \leq 500$) — the number of test cases.

The only line of each test case contains a single string $s$ ($1 \leq |s| \leq 500$) consisting of characters $\texttt{0}$ and $\texttt{1}$, where $|s|$ denotes the length of the string $s$.

Output

For each test case, output a single integer — the minimum number of pieces needed to be able to rearrange the string into a sorted binary string.

Example

input

6
11010
00000000
1
10
0001111
0110

output

3
1
1
2
1
2

Note

The first test case is pictured in the statement. It can be proven that you can’t use fewer than $3$ pieces.

In the second and third test cases, the binary string is already sorted, so only $1$ piece is needed.

In the fourth test case, you need to make a single cut between the two characters and rearrange them to make the string $\texttt{01}$.

翻译

您将获得一个二进制字符串 $^{\dagger}$ 。请找出需要将其切成的最小块数，以便将所得块重新排列成排序的二进制字符串。

注意：

• 每个角色必须恰好位于其中一个棋子中；
• 这些片段必须是原始字符串的连续子串；
• 您必须使用重新排列中的所有碎片。

$^{\dagger}$ 二进制字符串是由字符 $\texttt{0}$ 和 $\texttt{1}$ 组成的字符串。排序的二进制字符串是所有字符 $\texttt{0}$ 都位于所有字符 $\texttt{1}$ 之前的二进制字符串。

输入

第一行包含一个整数 $t$ ( $1 \leq t \leq 500$ ) - 测试用例的数量。

每个测试用例的唯一行包含一个字符串 $s$ ( $1 \leq |s| \leq 500$ )，由字符 $\texttt{0}$ 和 $\texttt{1}$ 组成，其中 $|s|$ 表示字符串 $s$ 的长度。

输出

对于每个测试用例，输出一个整数——能够将字符串重新排列成排序的二进制字符串所需的最小数量。

Example

input

6
11010
00000000
1
10
0001111
0110

output

3
1
1
2
1
2

笔记

第一个测试用例如声明中所示。可以证明使用的数量不能少于 $3$ 块。

在第二个和第三个测试用例中，二进制字符串已经排序，因此只需要 $1$ 块。

在第四个测试用例中，您需要在两个字符之间进行一次剪切并重新排列它们以形成字符串 $\texttt{01}$ 。

思路

​ 这道题目的目的可以转换为将所有的1放在一起,所有的0放在一起的最小分组数量,我们只需要随意找一个01组合**(001,00111这些都是),然后再将其他连续的0和1找出来即可,我们可以选择按照这种思路直接模拟,我还发现一种更加便捷的方式,就是求连续1和0的数量 - 1,但是对于10,110,11110000**这样的数据这种办法就不对,需要特判.

代码

#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <map>
#include <unordered_map>
#include <string>
#include <cmath>
#include <set>
#include <stack>
#include <vector>
#include <deque>
#include <bitset>
#include <cstdio>
#include <iomanip>
 
// #define int long long
#define ull unsigned long long
#define ed '\n'
#define fi first
#define se second
#define fore(i, l, r) for(int i = (int)(l); i <=(int)r; i++)
#define debug(x) cout << "#x = " << x << ed;
#define PI acos(-1)
#define E exp(1)
#define IOS ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define me0(st) memset(st, 0, sizeof st)
#define me3f(st) memset(st, 0x3f, sizeof st)
#define pdf(x) printf("%lf", double(x))
#define pif(x) printf("%d ",  int(x))
#define scf(x) printf("%d",  int(x))
#define re return 0
#define max(a, b) ((a) > (b) ? (a) : (b))
#define min(a, b) ((a) < (b) ? (a) : (b))
#define out(x, k) cout << fixed << setprecision(k) << x << ed
 
using namespace std;
 
typedef pair<int, int> PII;
typedef long long LL;
typedef double db;
 
 
const int INF = 1e9;
const int N = 1e5 + 10;
 
void solve() {
    string s;
    int ans = 1;
    cin >> s;
    int len = s.length();
    fore (i, 0, len - 2) {
        if (s[i] != s[i + 1]) ans++;
        if (i == len - 2 && ans == 2 && s[i + 1] == '0') ans++;
    }
    if (ans == 1) cout << 1 << ed;
    else cout << ans - 1 << ed;
}
int main()
{
    IOS;
    int _ = 1;
    cin >> _;
    
    while(_--) {
        solve();
    }
    
    re;
}

E. Find the Car

Timur is in a car traveling on the number line from point $0$ to point $n$. The car starts moving from point $0$ at minute $0$.

There are $k+1$ signs on the line at points $0, a_1, a_2, \dots, a_k$, and Timur knows that the car will arrive there at minutes $0, b_1, b_2, \dots, b_k$, respectively. The sequences $a$ and $b$ are strictly increasing with $a_k = n$.

Between any two adjacent signs, the car travels with a constant speed. Timur has $q$ queries: each query will be an integer $d$, and Timur wants you to output how many minutes it takes the car to reach point $d$, rounded down to the nearest integer.

Input

The first line contains a single integer $t$ ($1 \leq t \leq 10^4$) — the number of test cases.

The first line of each test case contains three integers $n$, $k$, and $q$, ($k \leq n \leq 10^9$; $1 \leq k, q \leq 10^5$) — the final destination, the number of points Timur knows the time for, and the number of queries respectively.

The second line of each test case contains $k$ integers $a_i$ ($1 \leq a_i \leq n$; $a_i < a_{i+1}$ for every $1 \leq i \leq k-1$; $a_k = n$).

The third line of each test case contains $k$ integers $b_i$ ($1 \leq b_i \leq 10^9$; $b_i < b_{i+1}$ for every $1 \leq i \leq k-1$).

Each of the following $q$ lines contains a single integer $d$ ($0 \leq d \leq n$) — the distance that Timur asks the minutes passed for.

The sum of $k$ over all test cases doesn’t exceed $10^5$, and the sum of $q$ over all test cases doesn’t exceed $10^5$.

Output

For each query, output a single integer — the number of minutes passed until the car reaches the point $d$, rounded down.

Example

input

4
10 1 3
10
10
0
6
7
10 2 4
4 10
4 7
6
4
2
7
1000000000 1 1
1000000000
1000000000
99999999
6 1 3
6
5
2
6
5

output

0 6 7 
5 4 2 5 
99999999 
1 5 4 

Note

For the first test case, the car goes from point $0$ to point $10$ in $10$ minutes, so the speed is $1$ unit per minute and:

• At point $0$, the time will be $0$ minutes.
• At point $6$, the time will be $6$ minutes.
• At point $7$, the time will be $7$ minutes.

For the second test case, between points $0$ and $4$, the car travels at a speed of $1$ unit per minute and between $4$ and $10$ with a speed of $2$ units per minute and:

• At point $6$, the time will be $5$ minutes.
• At point $4$, the time will be $4$ minutes.
• At point $2$, the time will be $2$ minutes.
• At point $7$, the time will be $5.5$ minutes, so the answer is $5$.

For the fourth test case, the car travels with $1.2$ units per minute, so the answers to the queries are:

• At point $2$, the time will be $1.66\dots$ minutes, so the answer is $1$.
• At point $6$, the time will be $5$ minutes.
• At point $5$, the time will be $4.16\dots$ minutes, so the answer is $4$.

翻译

Timur 乘坐一辆车沿着数轴从点 $0$ 行驶到点 $n$ 。汽车在 $0$ 分钟从点 $0$ 开始行驶。

线路上的 $0, a_1, a_2, \dots, a_k$ 点有 $k+1$ 标志，Timur 知道汽车将分别在 $0, b_1, b_2, \dots, b_k$ 分钟到达那里。序列 $a$ 和 $b$ 随着 $a_k = n$ 严格递增。

在任意两个相邻标志之间，汽车以恒定速度行驶。 Timur 有 $q$ 查询：每个查询都是一个整数 $d$ ，Timur 希望您输出汽车到达点 $d$ 需要多少分钟，向下舍入到最接近的整数。

输入

第一行包含一个整数 $t$ ( $1 \leq t \leq 10^4$ ) - 测试用例的数量。

每个测试用例的第一行包含三个整数 $n$ 、 $k$ 和 $q$ 、( $k \leq n \leq 10^9$ ; $1 \leq k, q \leq 10^5$ ) - 最终目的地、Timur 知道的时间点数量以及数量分别查询。

每个测试用例的第二行包含 $k$ 整数 $a_i$ （每个 $1 \leq i \leq k-1$ 为 $1 \leq a_i \leq n$ ； $a_i < a_{i+1}$ ； $a_k = n$ ）。

每个测试用例的第三行包含 $k$ 个整数 $b_i$ （每个 $1 \leq i \leq k-1$ 对应 $1 \leq b_i \leq 10^9$ ； $b_i < b_{i+1}$ ）。

以下每一行 $q$ 都包含一个整数 $d$ ( $0 \leq d \leq n$ ) - Timur 询问经过的分钟数的距离。

所有测试用例的 $k$ 总和不超过 $10^5$ ，所有测试用例的 $q$ 总和不超过 $10^5$ 。

输出

对于每个查询，输出一个整数 - 汽车到达点 $d$ 之前经过的分钟数，向下舍入。

Example

input

4
10 1 3
10
10
0
6
7
10 2 4
4 10
4 7
6
4
2
7
1000000000 1 1
1000000000
1000000000
99999999
6 1 3
6
5
2
6
5

output

0 6 7 
5 4 2 5 
99999999 
1 5 4 

笔记

对于第一个测试用例，汽车在 $10$ 分钟内从点 $0$ 行驶到点 $10$ ，因此速度为每分钟 $1$ 个单位，并且：

• 在点 $0$ ，时间将为 $0$ 分钟。
• 在点 $6$ ，时间将为 $6$ 分钟。
• 在点 $7$ ，时间将为 $7$ 分钟。

对于第二个测试用例，在点 $0$ 和 $4$ 之间，汽车以每分钟 $1$ 单位的速度行驶，在 $4$ 和 $10$ 之间，汽车以每分钟 $2$ 单位的速度行驶，并且：

• 在点 $6$ ，时间将为 $5$ 分钟。
• 在点 $4$ ，时间将为 $4$ 分钟。
• 在点 $2$ ，时间将为 $2$ 分钟。
• 在点 $7$ 处，时间将为 $5.5$ 分钟，因此答案为 $5$ 。

对于第四个测试用例，汽车以每分钟 $1.2$ 单位行驶，因此查询的答案为：

• 在点 $2$ 处，时间将为 $1.66\dots$ 分钟，因此答案为 $1$ 。
• 在点 $6$ ，时间将为 $5$ 分钟。
• 在点 $5$ 处，时间将为 $4.16\dots$ 分钟，因此答案为 $4$ 。

思路

​ 思路非常清晰,使用二分找到第一个<=d的位置r,然后再求r ~ r + 1的速度即可求出r ~ x需要经过的时间了.

代码

#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <map>
#include <unordered_map>
#include <string>
#include <cmath>
#include <set>
#include <stack>
#include <vector>
#include <deque>
#include <bitset>
#include <cstdio>
#include <iomanip>
 
// #define int long long
#define ull unsigned long long
#define ed '\n'
#define fi first
#define se second
#define fore(i, l, r) for(int i = (int)(l); i <=(int)r; i++)
#define debug(x) cout << "#x = " << x << ed;
#define PI acos(-1)
#define E exp(1)
#define IOS ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define me0(st) memset(st, 0, sizeof st)
#define me3f(st) memset(st, 0x3f, sizeof st)
#define pdf(x) printf("%lf", double(x))
#define pif(x) printf("%d ",  int(x))
#define scf(x) printf("%d",  int(x))
#define re return 0
#define max(a, b) ((a) > (b) ? (a) : (b))
#define min(a, b) ((a) < (b) ? (a) : (b))
#define out(x, k) cout << fixed << setprecision(k) << x << ed
 
using namespace std;
 
typedef pair<int, int> PII;
typedef long long LL;
typedef double db;
 
 
const int INF = 1e9;
const int N = 1e5 + 10;
LL a[N], b[N];
 
void solve() {
    LL n, k, q;
    cin >> n >> k >> q;
    fore (i, 1, k) cin >> a[i];
    a[k] = n;
    fore (i, 1, k) cin >> b[i];
    while (q--) {
        LL x;
        cin >> x;
        if (x == n) {
            cout << b[k] << " ";
            continue;
        }
        int l = 0, r = k;
        while (l < r) {
            int mid = (l + r + 1) >> 1;
            if (a[mid] <= x) l = mid;
            else r = mid - 1;
        }
 
        LL ans = b[r] + (x - a[r]) * (b[r + 1] - b[r]) / (a[r + 1] - a[r]);
        cout << ans << " ";
    }
    cout << ed;
}
int main()
{
    IOS;
    int _ = 1;
    cin >> _;
    
    while(_--) {
        solve();
    }
    
    re;
}

F. Circle Perimeter

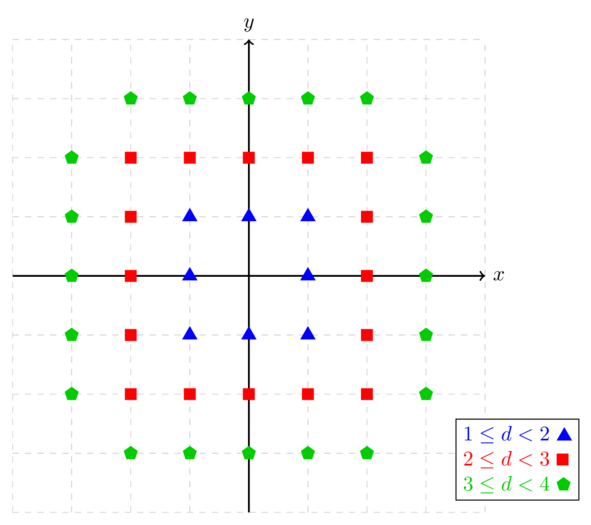
Given an integer $r$, find the number of lattice points that have a Euclidean distance from $(0, 0)$ greater than or equal to $r$ but strictly less than $r+1$.

A lattice point is a point with integer coordinates. The Euclidean distance from $(0, 0)$ to the point $(x,y)$ is $\sqrt{x^2 + y^2}$.

Input

The first line contains a single integer $t$ ($1 \leq t \leq 1000$) — the number of test cases.

The only line of each test case contains a single integer $r$ ($1 \leq r \leq 10^5$).

The sum of $r$ over all test cases does not exceed $10^5$.

Output

For each test case, output a single integer — the number of lattice points that have an Euclidean distance $d$ from $(0, 0)$ such that $r \leq d < r+1$.

Example

input

6
1
2
3
4
5
1984

output

8
16
20
24
40
12504

Note

The points for the first three test cases are shown below.

翻译

给定一个整数 $r$ ，找到与 $(0, 0)$ 大于或等于 $r$ 但严格小于 $r+1$ 的欧氏距离的格点数量。

格点是具有整数坐标的点。从 $(0, 0)$ 到点 $(x,y)$ 的欧几里得距离是 $\sqrt{x^2 + y^2}$ 。

输入

第一行包含一个整数 $t$ ( $1 \leq t \leq 1000$ ) - 测试用例的数量。

每个测试用例的唯一行包含一个整数 $r$ ( $1 \leq r \leq 10^5$ )。

所有测试用例的 $r$ 总和不超过 $10^5$ 。

输出

对于每个测试用例，输出一个整数 - 与 $(0, 0)$ 之间的欧几里德距离为 $d$ 且满足 $r \leq d < r+1$ 的晶格点数。

Example

input

6
1
2
3
4
5
1984

output

8
16
20
24
40
12504

笔记

前三个测试用例的要点如下所示。

思路

​

假设y从r+1 开始，右边的 A、B、C、D四个点都是比(0, 4)这个点低的，同时它们到(0,0)的距离都是 r+1；也就是说，当x遍历 0到 r+1 的时候，满足条件的点的纵坐标必定小于 y ，而这个 y 随着 x 的增大不断减小，直到0；

那么可以通过该方法来统计第一象限的整数点个数，最后乘上4即可.当然这种写法是比较保守的写法,不容易写错,大家也肯定很容易就可以知道另一种写法,就是求每个x对应的y1,y2,然后通过相减的方式求y1和y2之间的整数个数.但是我处理不好这个细节,还求各位给个写法.....

代码一(保守写法)

#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <map>
#include <unordered_map>
#include <string>
#include <cmath>
#include <set>
#include <stack>
#include <vector>
#include <deque>
#include <bitset>
#include <cstdio>
#include <iomanip>
 
// #define int long long
#define ull unsigned long long
#define ed '\n'
#define fi first
#define se second
#define fore(i, l, r) for(LL i = (LL)(l); i <=(LL)r; i++)
#define debug(x) cout << "#x = " << x << ed;
#define PI acos(-1)
#define E exp(1)
#define IOS ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define me0(st) memset(st, 0, sizeof st)
#define me3f(st) memset(st, 0x3f, sizeof st)
#define pdf(x) printf("%lf", double(x))
#define pif(x) printf("%d ",  int(x))
#define scf(x) printf("%d",  int(x))
#define re return 0
#define max(a, b) ((a) > (b) ? (a) : (b))
#define min(a, b) ((a) < (b) ? (a) : (b))
#define out(x, k) cout << fixed << setprecision(k) << x << ed
 
using namespace std;
 
typedef pair<int, int> PII;
typedef long long LL;
typedef double db;
 
 
const int INF = 1e9;
const int N = 1e5 + 10;
LL a[N], b[N];
 
void solve() {
    LL r;
    cin >> r;
    LL res = 0;
    LL j = r;
    LL MAX = pow(r + 1, 2);
    LL MIN = pow(r, 2);
    fore (i, 0, r) {
        while (i * i + j * j >= MAX) j--;
        LL k = j;
        while (k && i * i + k * k >= MIN) ++res, --k;
    }
    cout << res * 4 << ed;
}
 
int main()
{
    IOS;
    int _ = 1;
    cin >> _;
    
    while(_--) {
        solve();
    }
    
    re;
}

G. XOUR

You are given an array $a$ consisting of $n$ nonnegative integers.

You can swap the elements at positions $i$ and $j$ if $a_i\mathsf{XOR}a_j < 4$, where $\mathsf{XOR}$ is the bitwise XOR operation.

Find the lexicographically smallest array that can be made with any number of swaps.

An array $x$ is lexicographically smaller than an array $y$ if in the first position where $x$ and $y$ differ, $x_i < y_i$.

Input

The first line contains a single integer $t$ ($1 \leq t \leq 10^4$) — the number of test cases.

The first line of each test case contains a single integer $n$ ($1 \leq n \leq 2\cdot10^5$) — the length of the array.

The second line of each test case contains $n$ integers $a_i$ ($0 \leq a_i \leq 10^9$) — the elements of the array.

It is guaranteed that the sum of $n$ over all test cases does not exceed $2 \cdot 10^5$.

Output

For each test case, output $n$ integers — the lexicographically smallest array that can be made with any number of swaps.

Example

input

4
4
1 0 3 2
5
2 7 1 5 6
8
1 2 1 2 1 2 1 2
4
16 4 1 64

output

0 1 2 3 
1 5 2 6 7 
1 1 1 1 2 2 2 2 
16 4 1 64 

Note

For the first test case, you can swap any two elements, so we can produce the sorted array.

For the second test case, you can swap $2$ and $1$ (their $\mathsf{XOR}$ is $3$), $7$ and $5$ (their $\mathsf{XOR}$ is $2$), and $7$ and $6$ (their $\mathsf{XOR}$ is $1$) to get the lexicographically smallest array.

翻译

给您一个由 $n$ 个非负整数组成的数组 $a$ 。

如果是 $a_i\mathsf{XOR}a_j < 4$ ，则可以交换位置 $i$ 和 $j$ 的元素，其中 $\mathsf{XOR}$ 是按位异或运算。

找到可以通过任意次数的交换组成的字典顺序最小的数组。

如果在 $x$ 和 $y$ 不同的第一个位置 $x_i < y_i$ ，则数组 $x$ 按字典顺序小于数组 $y$ 。

输入

第一行包含一个整数 $t$ ( $1 \leq t \leq 10^4$ ) - 测试用例的数量。

每个测试用例的第一行包含一个整数 $n$ ( $1 \leq n \leq 2\cdot10^5$ ) - 数组的长度。

每个测试用例的第二行包含 $n$ 整数 $a_i$ ( $0 \leq a_i \leq 10^9$ ) - 数组的元素。

保证所有测试用例的 $n$ 之和不超过 $2 \cdot 10^5$ 。

输出

对于每个测试用例，输出 $n$ 整数 - 可以通过任意次数的交换生成的按字典顺序排列的最小数组。

Example

input

4
4
1 0 3 2
5
2 7 1 5 6
8
1 2 1 2 1 2 1 2
4
16 4 1 64

output

0 1 2 3 
1 5 2 6 7 
1 1 1 1 2 2 2 2 
16 4 1 64 

笔记

对于第一个测试用例，您可以交换任意两个元素，这样我们就可以生成排序后的数组。

对于第二个测试用例，您可以交换 $2$ 和 $1$ （它们的 $\mathsf{XOR}$ 是 $3$ ）、 $7$ 和 $5$ （它们的 $\mathsf{XOR}$ 是 $2$ ）以及 $7$ 和 $6$ （它们的 $\mathsf{XOR}$ 是 $1$ ）来获取按字典顺序排列的最小数组。

思路

​

代码