杂题——Cardboard for Pictures

Cardboard for Pictures

Mircea has $n$ pictures. The $i$-th picture is a square with a side length of $s_i$ centimeters.

He mounted each picture on a square piece of cardboard so that each picture has a border of $w$ centimeters of cardboard on all sides. In total, he used $c$ square centimeters of cardboard. Given the picture sizes and the value $c$, can you find the value of $w$?

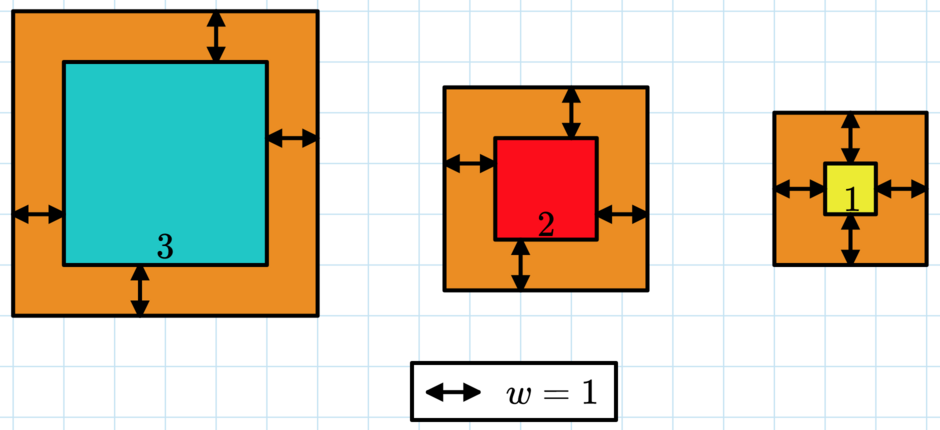A picture of the first test case. Here $c = 50 = 5^2 + 4^2 + 3^2$, so $w=1$ is the answer.

Please note that the piece of cardboard goes behind each picture, not just the border.

Input

The first line contains a single integer $t$ ($1 \leq t \leq 1000$) — the number of test cases.

The first line of each test case contains two positive integers $n$ ($1 \leq n \leq 2 \cdot 10^5$) and $c$ ($1 \leq c \leq 10^{18}$) — the number of paintings, and the amount of used square centimeters of cardboard.

The second line of each test case contains $n$ space-separated integers $s_i$ ($1 \leq s_i \leq 10^4$) — the sizes of the paintings.

The sum of $n$ over all test cases doesn’t exceed $2 \cdot 10^5$.

Additional constraint on the input: Such an integer $w$ exists for each test case.

Please note, that some of the input for some test cases won’t fit into 32-bit integer type, so you should use at least 64-bit integer type in your programming language (like long long for C++).

Output

For each test case, output a single integer — the value of $w$ ($w \geq 1$) which was used to use exactly $c$ squared centimeters of cardboard.

Example

input

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
10
3 50
3 2 1
1 100
6
5 500
2 2 2 2 2
2 365
3 4
2 469077255466389
10000 2023
10 635472106413848880
9181 4243 7777 1859 2017 4397 14 9390 2245 7225
7 176345687772781240
9202 9407 9229 6257 7743 5738 7966
14 865563946464579627
3654 5483 1657 7571 1639 9815 122 9468 3079 2666 5498 4540 7861 5384
19 977162053008871403
9169 9520 9209 9013 9300 9843 9933 9454 9960 9167 9964 9701 9251 9404 9462 9277 9661 9164 9161
18 886531871815571953
2609 10 5098 9591 949 8485 6385 4586 1064 5412 6564 8460 2245 6552 5089 8353 3803 3764

output

1
2
3
4
5
6
7
8
9
10
1
2
4
5
7654321
126040443
79356352
124321725
113385729
110961227

Note

The first test case is explained in the statement.

For the second test case, the chosen $w$ was $2$, thus the only cardboard covers an area of $c = (2 \cdot 2 + 6)^2 = 10^2 = 100$ squared centimeters.

For the third test case, the chosen $w$ was $4$, which obtains the covered area $c = (2 \cdot 4 + 2)^2 \times 5 = 10^2 \times 5 = 100 \times 5 = 500$ squared centimeters.

翻译

Mircea 有 $n$ 照片。第 $i$ 张图片是一个边长为 $s _ i$ 厘米的正方形。

他将每张图片安装在一块方形纸板上，以便每张图片的四面都有 $w$ 厘米的纸板边框。他总共使用了 $c$ 平方厘米的纸板。给定图片尺寸和值 $c$ ，您能找到 $w$ 的值吗？

第一个测试用例的图片。这里是 $c = 50 = 5^2 + 4^2 + 3^2$ ，所以答案是 $w=1$ 。

请注意，纸板位于每张图片的后面，而不仅仅是边框。

输入

第一行包含一个整数 $t$ ( $1 \leq t \leq 1000$ ) - 测试用例的数量。

每个测试用例的第一行包含两个正整数 $n$ ( $1 \leq n \leq 2 \cdot 10^5$ ) 和 $c$ ( $1 \leq c \leq 10^{18}$ ) - 绘画的数量以及使用的平方厘米纸板的数量。

每个测试用例的第二行包含 $n$ 以空格分隔的整数 $s _ i$ ( $1 \leq s _ i \leq 10^4$ ) - 绘画的尺寸。

所有测试用例的 $n$ 总和不超过 $2 \cdot 10^5$ 。

对输入的附加约束： 每个测试用例都存在这样一个整数 $w$ 。

请注意，某些测试用例的某些输入不适合 32 位整数类型，因此您应该在编程语言中至少使用 64 位整数类型(例如 C++ 的 long long)。

输出

对于每个测试用例，输出一个整数 - $w$ ( $w \geq 1$ ) 的值，用于使用恰好 $c$ 平方厘米的纸板。

Example

input

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
10
3 50
3 2 1
1 100
6
5 500
2 2 2 2 2
2 365
3 4
2 469077255466389
10000 2023
10 635472106413848880
9181 4243 7777 1859 2017 4397 14 9390 2245 7225
7 176345687772781240
9202 9407 9229 6257 7743 5738 7966
14 865563946464579627
3654 5483 1657 7571 1639 9815 122 9468 3079 2666 5498 4540 7861 5384
19 977162053008871403
9169 9520 9209 9013 9300 9843 9933 9454 9960 9167 9964 9701 9251 9404 9462 9277 9661 9164 9161
18 886531871815571953
2609 10 5098 9591 949 8485 6385 4586 1064 5412 6564 8460 2245 6552 5089 8353 3803 3764

output

1
2
3
4
5
6
7
8
9
10
1
2
4
5
7654321
126040443
79356352
124321725
113385729
110961227

笔记

第一个测试用例在声明中进行了解释。

对于第二个测试用例，选择的 $w$ 是 $2$ ，因此唯一的纸板覆盖了 $c = (2 \cdot 2 + 6)^2 = 10^2 = 100$ 平方厘米的面积。

对于第三个测试用例，选择的 $w$ 是 $4$ ，它获得覆盖面积 $c = (2 \cdot 4 + 2)^2 \times 5 = 10^2 \times 5 = 100 \times 5 = 500$ 平方厘米。

思路

​ 纯粹的数学公式推导的一道题目.这道题目比较恶心的一个地方关键在于其在判断的时候需要强制类型转换为__int128类型,开unsigned long long也不够.

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
// (k1 + 2w)^2 + (k2 + 2w)^2 + (k3 + 2w)^2 ...= k
// 展开: (k1^2 + k2^2 + ... + kn^2) + 4w(k1 + k2 + k3 + ... + kn) + n4w^2 = k
// k1w + k2w + ... + knw + nw^2 = k - k1^2 - k2^2 ... / 4
// w(k1 + k2 + ... + kn) + nw^2 = k - k1^2 - k2^2 ... / 4
#include <bits/stdc++.h>
using namespace std;
typedef unsigned long long LL;
typedef __int128 ULL;
const LL INF = 0x3f3f3f3f;
LL n, c, sum;

int main()
{
    ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
    int t;
    cin >> t;
    while (t--) {
        cin >> n >> c;
        sum = 0;
        for (int i = 1; i <= n; i ++) {
            LL x;
            cin >> x;
            c -= x * x;
            sum += x;
        }
        c /= 4;
        // cout << c << '\n';
        LL l = 1, r = INF;
        while (l < r) {
            LL mid = (l + r + 1) >> 1;
            if (ULL(sum) * mid + ULL(n) * mid * mid <= c) l = mid;
            else r = mid - 1;
        }

        cout << r << '\n';
    }
    return 0;
}