算法练习专栏——Codeforces——Codeforces Round 871 (Div. 4)

D. Gold Rush

原题

Initially you have a single pile with $n$ gold nuggets. In an operation you can do the following:

  • Take any pile and split it into two piles, so that one of the resulting piles has exactly twice as many gold nuggets as the other. (All piles should have an integer number of nuggets.)

One possible move is to take a pile of size $6$ and split it into piles of sizes $2$ and $4$, which is valid since $4$ is twice as large as $2$.

Can you make a pile with exactly $m$ gold nuggets using zero or more operations?

Input

The first line contains an integer $t$ ($1 \leq t \leq 1000$) — the number of test cases.

The only line of each test case contains two integers $n$ and $m$ ($1 \leq n, m \leq 10^7$) — the starting and target pile sizes, respectively.

Output

For each test case, output “YES” if you can make a pile of size exactly $m$, and “NO” otherwise.

You can output the answer in any case (for example, the strings “yEs”, “yes”, “Yes” and “YES” will be recognized as a positive answer).

Example

input

1
2
3
4
5
6
7
8
9
10
11
12
11
6 4
9 4
4 2
18 27
27 4
27 2
27 10
1 1
3 1
5 1
746001 2984004

output

1
2
3
4
5
6
7
8
9
10
11
YES
YES
NO
NO
YES
YES
NO
YES
YES
NO
NO

Note

The first test case is pictured in the statement. We can make a pile of size $4$.

In the second test case, we can perform the following operations: ${\color{red}{9}} \to {\color{red}{6},3} \to {4,2,3}$. The pile that is split apart is colored red before each operation.

In the third test case, we can’t perform a single operation.

In the fourth test case, we can’t end up with a larger pile than we started with.*

翻译

最初，您有一堆 $n$ 金块。在操作中您可以执行以下操作：

  • 将任意一堆金块分成两堆，这样其中一堆金块的数量恰好是另一堆金块的两倍。 （所有堆应该有整数个金块。）

一种可能的做法是取出一堆大小为 $6$ 的堆，并将其分成大小为 $2$ 和 $4$ 的堆，这是有效的，因为 $4$ 是 $2$ 的两倍。

您可以使用零次或多次操作将准确的 $m$ 金块堆成一堆吗？

输入

第一行包含一个整数 $t$ ( $1 \leq t \leq 1000$ ) - 测试用例的数量。

每个测试用例的唯一行包含两个整数 $n$ 和 $m$ ( $1 \leq n, m \leq 10^7$ ) - 分别是起始堆大小和目标堆大小。

输出

对于每个测试用例，如果您可以制作一堆大小恰好为 $m$ 的堆，则输出“YES”，否则输出“NO”。

您可以在任何情况下输出答案（例如，字符串“yEs”、“yes”、“Yes”和“YES”将被识别为肯定答案）。

Example

input

1
2
3
4
5
6
7
8
9
10
11
12
11
6 4
9 4
4 2
18 27
27 4
27 2
27 10
1 1
3 1
5 1
746001 2984004

output

1
2
3
4
5
6
7
8
9
10
11
YES
YES
NO
NO
YES
YES
NO
YES
YES
NO
NO

笔记

第一个测试用例如声明中所示。我们可以制作一堆大小为 $4$ 的堆。

在第二个测试用例中，我们可以执行以下操作： ${\color{red}{9}} \to {\color{red}{6},3} \to {4,2,3}$ 。每次操作前，被分开的一堆都被涂成红色。

在第三个测试用例中，我们无法执行单个操作。

在第四个测试用例中，我们最终得到的堆不会比开始时更大。

思路

​ 对每个数进行DFS深搜一下就ok了.

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include <bits/stdc++.h>
 
using namespace std;
int n, m;
 
bool check(int x) {
    if (x == m) return true;
    if (x % 3) return false;
 
    if (check(x / 3 * 2)) return true;
    if (check(x / 3)) return true;
 
    return false;
}
int main()
{
    ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
    int t;
    cin >> t;
    while (t--) {
        cin >> n >> m;
        if (check(n)) cout << "YES\n";
        else cout << "NO\n";
    }
 
    return 0;
}

E. The Lakes

You are given an $n \times m$ grid $a$ of non-negative integers. The value $a_{i,j}$ represents the depth of water at the $i$-th row and $j$-th column.

A lake is a set of cells such that:

  • each cell in the set has $a_{i,j} > 0$, and
  • there exists a path between any pair of cells in the lake by going up, down, left, or right a number of times and without stepping on a cell with $a_{i,j} = 0$.

The volume of a lake is the sum of depths of all the cells in the lake.

Find the largest volume of a lake in the grid.

Input

The first line contains a single integer $t$ ($1 \leq t \leq 10^4$) — the number of test cases.

The first line of each test case contains two integers $n, m$ ($1 \leq n, m \leq 1000$) — the number of rows and columns of the grid, respectively.

Then $n$ lines follow each with $m$ integers $a_{i,j}$ ($0 \leq a_{i,j} \leq 1000$) — the depth of the water at each cell.

It is guaranteed that the sum of $n \cdot m$ over all test cases does not exceed $10^6$.

Output

For each test case, output a single integer — the largest volume of a lake in the grid.

Example

input

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
5
3 3
1 2 0
3 4 0
0 0 5
1 1
0
3 3
0 1 1
1 0 1
1 1 1
5 5
1 1 1 1 1
1 0 0 0 1
1 0 5 0 1
1 0 0 0 1
1 1 1 1 1
5 5
1 1 1 1 1
1 0 0 0 1
1 1 4 0 1
1 0 0 0 1
1 1 1 1 1

output

1
2
3
4
5
10
0
7
16
21

思路

​ 没啥思路,就是一个洪水铺盖算法,实际就是一个BFS没了.非常适合新手练习的一道试题.

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <map>
#include <unordered_map>
#include <string>
#include <cmath>
#include <set>
#include <stack>
#include <vector>
#include <deque>
#include <bitset>
#include <cstdio>
#include <iomanip>

// #define int long long
#define ull unsigned long long
#define ed '\n'
#define fi first
#define se second
#define fore(i, l, r) for(int i = (int)(l); i <=(int)r; i++)
#define debug(x) cout << "#x = " << x << ed;
#define PI acos(-1)
#define E exp(1)
#define IOS ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define me0(st) memset(st, 0, sizeof st)
#define me3f(st) memset(st, 0x3f, sizeof st)
#define pdf(x) printf("%lf", double(x))
#define pif(x) printf("%d ",  int(x))
#define scf(x) printf("%d",  int(x))
#define re return 0
#define max(a, b) ((a) > (b) ? (a) : (b))
#define min(a, b) ((a) < (b) ? (a) : (b))
#define out(x, k) cout << fixed << setprecision(k) << x << ed

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;
typedef double db;


const int INF = 1e9;
const int N = 1e3 + 10;
int a[N][N];
bool st[N][N];
int dx[4] = {1, 0, -1, 0}, dy[4] = {0, 1, 0, -1};
int n, m;

LL BFS(int x, int y) {
    st[x][y] = true;
    queue<PII> q;
    q.push({x, y});
    LL ans = a[x][y];
    while (q.size()){
        auto t = q.front();
        q.pop();
        int xx = t.fi, yy = t.se;
        
        
        fore (i, 0, 3) {
            int x2 = xx + dx[i], y2 = yy + dy[i];
            if (x2 >= 1 && x2 <= n && y2 >= 1 && y2 <= m && !st[x2][y2] && a[x2][y2]) {
                st[x2][y2] = true;
                q.push({x2, y2});
                ans += a[x2][y2];
            }
        }
    }

    return ans;
}
void solve() {
    memset(st, false, sizeof st);
    LL res = 0;
    cin >> n >> m;
    fore (i, 1, n) {
        fore (j, 1, m) cin >> a[i][j];
    }

    fore (i, 1, n) {
        fore (j, 1, m) {
            if (!st[i][j] && a[i][j]) {
                LL tt = BFS(i, j);
                res = max(res, tt); 
            }
        }
    }

    cout << res << ed;
}
int main()
{
    IOS;
    int _ = 1;
    cin >> _;
    
    while(_--) {
        solve();
    }
    
    re;
}

F:Forever Winter

A snowflake graph is generated from two integers $x$ and $y$, both greater than $1$, as follows:

  • Start with one central vertex.
  • Connect $x$ new vertices to this central vertex.
  • Connect $y$ new vertices to each of these $x$ vertices.

For example, below is a snowflake graph for $x=5$ and $y=3$.

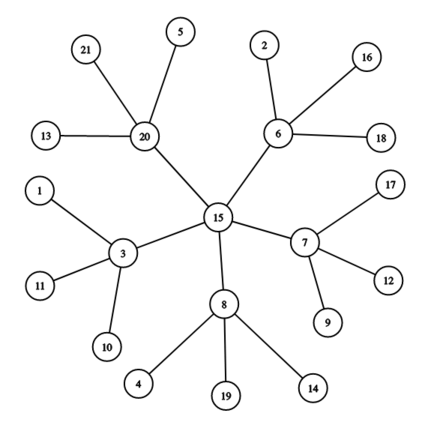
The snowflake graph above has a central vertex $15$, then $x=5$ vertices attached to it ($3$, $6$, $7$, $8$, and $20$), and then $y=3$ vertices attached to each of those.

Given a snowflake graph, determine the values of $x$ and $y$.

Input

The first line contains a single integer $t$ ($1 \leq t \leq 1000$) — the number of test cases.

The first line of each test case contains two integers $n$ and $m$ ($2 \leq n \leq 200$; $1 \leq m \leq \min\left(1000, \frac{n(n-1)}{2}\right)$) — the number of vertices and edges in the graph, respectively.

The next $m$ lines each contain two integers each $u$ and $v$ ($1 \leq u, v \leq n$, $u \neq v$) — the numbers of vertices connected by an edge. The graph does not contain multiple edges and self-loops.

It is guaranteed that this graph is a snowflake graph for some integers $x$ and $y$ both greater than $1$.

Output

For each test case, on a separate line output the values of $x$ and $y$, in that order, separated by a space.

Example

input

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
3
21 20
21 20
5 20
13 20
1 3
11 3
10 3
4 8
19 8
14 8
9 7
12 7
17 7
18 6
16 6
2 6
6 15
7 15
8 15
20 15
3 15
7 6
1 2
1 3
2 4
2 5
3 6
3 7
9 8
9 3
3 6
6 2
2 1
5 2
2 7
4 3
3 8

output

1
2
3
5 3
2 2
2 3

Note

The first test case is pictured in the statement. Note that the output 3 5 is incorrect, since $x$ should be output before $y$.

翻译

雪花图由两个整数 $x$ 和 $y$ 生成，两者都大于 $1$ ，如下所示：

  • 从一个中心顶点开始。
  • 将 $x$ 个新顶点连接到该中心顶点。
  • 将 $y$ 个新顶点连接到这些 $x$ 个顶点的每个。

例如，下面是 $x=5$ 和 $y=3$ 的雪花图。

上面的雪花图有一个中心顶点 $15$ ，然后附加了 $x=5$ 个顶点（ $3$ 、 $6$ 、 $7$ 、 $8$ 和 $20$ ），然后附加了 $y=3$ 个顶点对其中每一个。

给定一个雪花图，确定 $x$ 和 $y$ 的值。

输入

第一行包含一个整数 $t$ ( $1 \leq t \leq 1000$ ) - 测试用例的数量。

每个测试用例的第一行包含两个整数 $n$ 和 $m$ ( $2 \leq n \leq 200$ ; $1 \leq m \leq \min\left(1000, \frac{n(n-1)}{2}\right)$ ) - 分别是图中的顶点数和边数。

接下来的 $m$ 行每行包含两个整数，分别为 $u$ 和 $v$ ( $1 \leq u, v \leq n$ , $u \neq v$ ) - 由边连接的顶点数。该图不包含多条边和自环。

对于某些整数 $x$ 和 $y$ 都大于 $1$ ，可以保证该图是雪花图。

输出

对于每个测试用例，在单独的行上按顺序输出 $x$ 和 $y$ 的值，并用空格分隔。

Example

input

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
3
21 20
21 20
5 20
13 20
1 3
11 3
10 3
4 8
19 8
14 8
9 7
12 7
17 7
18 6
16 6
2 6
6 15
7 15
8 15
20 15
3 15
7 6
1 2
1 3
2 4
2 5
3 6
3 7
9 8
9 3
3 6
6 2
2 1
5 2
2 7
4 3
3 8

output

1
2
3
5 3
2 2
2 3

笔记

第一个测试用例如声明中所示。请注意，输出 3 5 不正确，因为 $x$ 应该在 $y$ 之前输出。

思路

​ 从我的角度看这道题目,虽然看起来很像一道图论的题目,但是我操作完之后似乎感觉不到任何图的知识,我感觉我用到的是结点个数的统计,是一种找不同,特判的思维,用到一点点数学公式,然后没了.

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <map>
#include <unordered_map>
#include <string>
#include <cmath>
#include <set>
#include <stack>
#include <vector>
#include <deque>
#include <bitset>
#include <cstdio>
#include <iomanip>

// #define int long long
#define ull unsigned long long
#define ed '\n'
#define fi first
#define se second
#define fore(i, l, r) for(int i = (int)(l); i <=(int)r; i++)
#define debug(x) cout << "#x = " << x << ed;
#define PI acos(-1)
#define E exp(1)
#define IOS ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define me0(st) memset(st, 0, sizeof st)
#define me3f(st) memset(st, 0x3f, sizeof st)
#define pdf(x) printf("%lf", double(x))
#define pif(x) printf("%d ",  int(x))
#define scf(x) printf("%d",  int(x))
#define re return 0
#define max(a, b) ((a) > (b) ? (a) : (b))
#define min(a, b) ((a) < (b) ? (a) : (b))
#define out(x, k) cout << fixed << setprecision(k) << x << ed

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;
typedef double db;


const int INF = 1e9;
const int N = 510, M = 2e3 + 10;
int n, m;
int h[M];

void solve() {
    memset(h, 0, sizeof h);
    cin >> n >> m;
    set<int> p;
    LL res = 0;
    fore (i, 1, m) {
        int a, b;
        cin >> a >> b;
        h[a]++;
        h[b]++;
        p.insert(a);
        p.insert(b);
    } 
    
    for (auto k : p){
        if (h[k] == 1) res++;
    }

    LL y = n - res - 1;
    LL x = res / y;

    cout << y << " " << x << ed;
}
int main()
{
    IOS;
    int _ = 1;
    cin >> _;
    
    while(_--) {
        solve();
    }
    
    re;
}

// x * y = 15
// y = n - 15 - 1 = 5


G. Hits Different

In a carnival game, there is a huge pyramid of cans with $2023$ rows, numbered in a regular pattern as shown.

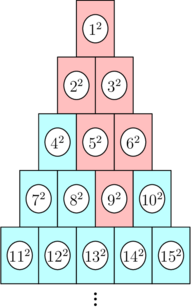
If can $9^2$ is hit initially, then all cans colored red in the picture above would fall.

You throw a ball at the pyramid, and it hits a single can with number $n^2$. This causes all cans that are stacked on top of this can to fall (that is, can $n^2$ falls, then the cans directly above $n^2$ fall, then the cans directly above those cans, and so on). For example, the picture above shows the cans that would fall if can $9^2$ is hit.

What is the sum of the numbers on all cans that fall? Recall that $n^2 = n \times n$.

Input

The first line contains an integer $t$ ($1 \leq t \leq 1000$) — the number of test cases.

The only line of each test case contains a single integer $n$ ($1 \leq n \leq 10^6$) — it means that the can you hit has label $n^2$.

Output

For each test case, output a single integer — the sum of the numbers on all cans that fall.

Please note, that the answer for some test cases won’t fit into 32-bit integer type, so you should use at least 64-bit integer type in your programming language (like long long for C++). For all valid inputs, the answer will always fit into 64-bit integer type.

Example

input

1
2
3
4
5
6
7
8
9
10
11
10
9
1
2
3
4
5
6
10
1434
1000000

output

1
2
3
4
5
6
7
8
9
10
156
1
5
10
21
39
46
146
63145186
58116199242129511

Note

The first test case is pictured in the statement. The sum of the numbers that fall is

$$
1^2 + 2^2 + 3^2 + 5^2 + 6^2 + 9^2 = 1 + 4 + 9 + 25 + 36 + 81 = 156.
$$

In the second test case, only the can labeled $1^2$ falls, so the answer is $1^2=1$.

In the third test case, the cans labeled $1^2$ and $2^2$ fall, so the answer is $1^2+2^2=1+4=5$.

In the fourth test case, the cans labeled $1^2$ and $3^2$ fall, so the answer is $1^2+3^2=1+9=10$.

In the fifth test case, the cans labeled $1^2$, $2^2$, and $4^2$ fall, so the answer is $1^2+2^2+4^2=1+4+16=21$.

翻译

在嘉年华游戏中，有一个巨大的金字塔金字塔，有 $2023$ 行，按如图所示的规则模式编号。

如果罐子 $9^2$ 最初被击中，那么上图中所有红色的罐子都会掉落。

你向金字塔扔一个球，它会击中一个编号为 $n^2$ 的罐子。这会导致堆叠在该罐顶上的所有罐子掉落(即罐子 $n^2$ 掉落，然后直接位于 $n^2$ 上方的罐子掉落，然后直接位于这些罐子上方的罐子掉落，依此类推)。例如，上图显示，如果罐头 $9^2$ 被击中，罐头就会掉落。

掉落的所有罐子上的数字的总和是多少？回想一下 $n^2 = n \times n$ 。

输入

第一行包含一个整数 $t$ ( $1 \leq t \leq 1000$ ) - 测试用例的数量。

每个测试用例的唯一行包含一个整数 $n$ ( $1 \leq n \leq 10^6$ ) - 这意味着您点击的罐头具有标签 $n^2$ 。

输出

对于每个测试用例，输出一个整数——所有掉落的罐子上的数字之和。

请注意，某些测试用例的答案不适合 32 位整数类型，因此您应该在编程语言中至少使用 64 位整数类型(例如 C++ 的 long long)。对于所有有效输入，答案将始终适合 64 位整数类型。

Example

input

1
2
3
4
5
6
7
8
9
10
11
10
9
1
2
3
4
5
6
10
1434
1000000

output

1
2
3
4
5
6
7
8
9
10
156
1
5
10
21
39
46
146
63145186
58116199242129511

笔记

第一个测试用例如声明中所示。落下的数字之和为

$
1^2 + 2^2 + 3^2 + 5^2 + 6^2 + 9^2 = 1 + 4 + 9 + 25 + 36 + 81 = 156.
$

在第二个测试用例中，只有标记为 $1^2$ 的罐子掉落，因此答案为 $1^2=1$ 。

在第三个测试用例中，标记为 $1^2$ 和 $2^2$ 的罐子掉落，因此答案为 $1^2+2^2=1+4=5$ 。

在第四个测试用例中，标记为 $1^2$ 和 $3^2$ 的罐子掉落，因此答案为 $1^2+3^2=1+9=10$ 。

在第五个测试用例中，标记为 $1^2$ 、 $2^2$ 和 $4^2$ 的罐子掉落，因此答案为 $1^2+2^2+4^2=1+4+16=21$ 。

思路

​ 参考原文

思路：改成正三角形比较直观易懂。如图：

image-20240515200217706

这样即可找出规律：

所求倒下的木块编号，即该点的主对角线左上部分加上该点上面的点的左上部分所有的木块。

这样可以前缀和预处理出该点的左上角部分加本身的s数组。

不可以把前缀和设置成左上角加正上方因为这样会重复。

image-20240515200227387

如若如此5^2的点的前缀和中和9^2的前缀和中

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int maxn=1e6+8;
int f[2040][2040];
int s[2040][2040];
map<int,pair<int,int> > mp;
int t,n;
int cnt=1;
void get(){
    for(int i=1;i<=2023;i++){
        for(int j=1;j<=i;j++){
            f[i][j]=cnt*cnt;
            s[i][j]=s[i-1][j-1]+f[i][j];//斜向前缀和
            mp[cnt++]={i,j};//找出每个数在正三角对应的位置
        }
    }
}//变换直角三角形找出规律
signed main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    get();
    cin>>t;
    while(t--){
        cin>>n;
        int x=mp[n].first;
        int y=mp[n].second;
        int sum=0;
        while(x>=1){
            sum+=s[x][y];
            x--;
        }//每一次加上上面的主对角线
        cout<<sum<<"\n";
    }
    return 0;
}