杂题——Bouncy Ball

Bouncy Ball

原题

You are given a room that can be represented by a $n \times m$ grid. There is a ball at position $(i_1, j_1)$ (the intersection of row $i_1$ and column $j_1$), and it starts going diagonally in one of the four directions:

  • The ball is going down and right, denoted by $\texttt{DR}$; it means that after a step, the ball’s location goes from $(i, j)$ to $(i+1, j+1)$.
  • The ball is going down and left, denoted by $\texttt{DL}$; it means that after a step, the ball’s location goes from $(i, j)$ to $(i+1, j-1)$.
  • The ball is going up and right, denoted by $\texttt{UR}$; it means that after a step, the ball’s location goes from $(i, j)$ to $(i-1, j+1)$.
  • The ball is going up and left, denoted by $\texttt{UL}$; it means that after a step, the ball’s location goes from $(i, j)$ to $(i-1, j-1)$.

After each step, the ball maintains its direction unless it hits a wall (that is, the direction takes it out of the room’s bounds in the next step). In this case, the ball’s direction gets flipped along the axis of the wall; if the ball hits a corner, both directions get flipped. Any instance of this is called a bounce. The ball never stops moving.

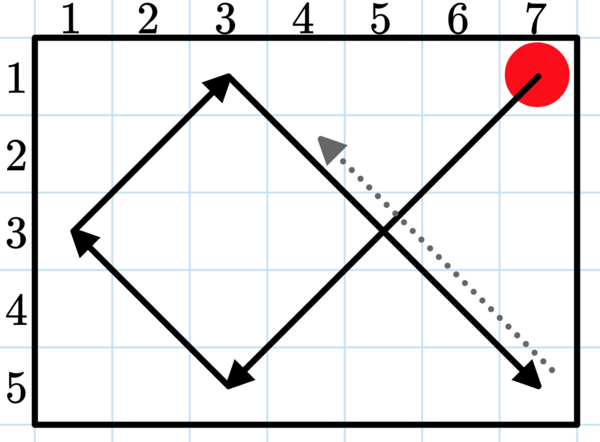
In the above example, the ball starts at $(1, 7)$ and goes $\texttt{DL}$ until it reaches the bottom wall, then it bounces and continues in the direction $\texttt{UL}$. After reaching the left wall, the ball bounces and continues to go in the direction $\texttt{UR}$. When the ball reaches the upper wall, it bounces and continues in the direction $\texttt{DR}$. After reaching the bottom-right corner, it bounces once and continues in direction $\texttt{UL}$, and so on.

Your task is to find how many bounces the ball will go through until it reaches cell $(i_2, j_2)$ in the room, or report that it never reaches cell $(i_2, j_2)$ by printing $-1$.

Note that the ball first goes in a cell and only after that bounces if it needs to.

Input

The first line contains a single integer $t$ ($1 \leq t \leq 1000$) — the number of test cases.

The first line of each test case contains six integers and a string $n, m, i_1, j_1, i_2, j_2, d$ ($2 \leq n, m \leq 25000$; $1 \leq i_1, i_2 \leq n$; $1 \leq j_1, j_2 \leq m$; $d \in{ \texttt{DR}, \texttt{DL}, \texttt{UR}, \texttt{UL}}$) — the dimensions of the grid, the starting coordinates of the ball, the coordinates of the final cell and the starting direction of the ball.

It is guaranteed that the sum of $n \cdot m$ over all test cases does not exceed $5 \cdot 10^4$.

Output

For each test case, output a single integer — the number of bounces the ball does until it reaches cell $(i_2, j_2)$ for the first time, or $-1$ if the ball never reaches the final cell.

Example

input

1
2
3
4
5
6
7
6
5 7 1 7 2 4 DL
5 7 1 7 3 2 DL
3 3 1 3 2 2 UR
2 4 2 1 2 2 DR
4 3 1 1 1 3 UL
6 4 1 2 3 4 DR

output

1
2
3
4
5
6
3
-1
1
-1
4
0

翻译

您将获得一个可以用 $n \times m$ 网格表示的房间。在位置 $(i_1, j_1)$ （行 $i_1$ 和列 $j_1$ 的交集）处有一个球，它开始沿四个方向之一沿对角线移动：

  • 球向右下方移动，记为 $\texttt{DR}$ ；这意味着一步之后，球的位置从 $(i, j)$ 变为 $(i+1, j+1)$ 。
  • 球向左下方移动，记为 $\texttt{DL}$ ；这意味着一步之后，球的位置从 $(i, j)$ 变为 $(i+1, j-1)$ 。
  • 球向右上方移动，记为 $\texttt{UR}$ ；这意味着一步之后，球的位置从 $(i, j)$ 变为 $(i-1, j+1)$ 。
  • 球向上并向左移动，记为 $\texttt{UL}$ ；这意味着一步之后，球的位置从 $(i, j)$ 变为 $(i-1, j-1)$ 。

每一步之后，球都会保持其方向，除非它撞到墙壁（也就是说，该方向在下一步中将其带出房间的边界）。在这种情况下，球的方向沿着墙的轴线翻转；如果球撞到角落，两个方向都会翻转。任何这种情况都称为反弹。球永远不会停止移动。

在上面的示例中，球从 $(1, 7)$ 开始，行进 $\texttt{DL}$ 直到到达底墙，然后弹跳并继续朝 $\texttt{UL}$ 方向运动。到达左侧墙壁后，球弹起并继续朝 $\texttt{UR}$ 方向移动。当球到达上墙时，它会弹起并继续朝 $\texttt{DR}$ 方向移动。到达右下角后，它会弹一次并继续朝 $\texttt{UL}$ 方向移动，依此类推。

您的任务是找出球在到达房间中的单元格 $(i_2, j_2)$ 之前将经历多少次弹跳，或者通过打印 $-1$ 报告它从未到达单元格 $(i_2, j_2)$ 。

请注意，球首先进入一个单元格，然后只有在需要时才会反弹。

输入

第一行包含一个整数 $t$ ( $1 \leq t \leq 1000$ ) - 测试用例的数量。

每个测试用例的第一行包含六个整数和一个字符串 $n, m, i_1, j_1, i_2, j_2, d$ ( $2 \leq n, m \leq 25000$ ; $1 \leq i_1, i_2 \leq n$ ; $1 \leq j_1, j_2 \leq m$ ; $d \in{ \texttt{DR}, \texttt{DL}, \texttt{UR}, \texttt{UL}}$ ) - 网格的尺寸，球的起始坐标，最后一个单元格和球的起始方向。

保证所有测试用例的 $n \cdot m$ 之和不超过 $5 \cdot 10^4$ 。

输出

对于每个测试用例，输出一个整数 - 球第一次到达单元格 $(i_2, j_2)$ 之前的弹跳次数，如果球从未到达最后一个单元格，则输出 $-1$ 。

Example

input

1
2
3
4
5
6
7
6
5 7 1 7 2 4 DL
5 7 1 7 3 2 DL
3 3 1 3 2 2 UR
2 4 2 1 2 2 DR
4 3 1 1 1 3 UL
6 4 1 2 3 4 DR

output

1
2
3
4
5
6
3
-1
1
-1
4
0

思路

​ 模拟这个点走的过程，如果走到一个之前走到的状态就说明陷入了循环，此时就是无解，状态可以用坐标和方向来表示，坐标 = (横坐标 - 1) * 列数 + 列坐标.

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <map>
#include <unordered_map>
#include <string>
#include <cmath>
#include <set>
#include <stack>
#include <vector>
#include <deque>
#include <bitset>
#include <cstdio>
#include <iomanip>

// #define int long long
#define ull unsigned long long
#define ed '\n'
#define x first
#define y second
#define fore(i, l, r) for(int i = (int)(l); i <=(int)r; i++)
#define debug(x) cout << "#x = " << x << ed;
#define PI acos(-1)
#define E exp(1)
#define IOS ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define me0(st) memset(st, 0, sizeof st)
#define me3f(st) memset(st, 0x3f, sizeof st)
#define pdf(x) printf("%lf", double(x))
#define pif(x) printf("%d ",  int(x))
#define scf(x) printf("%d",  int(x))
#define re return 0
#define max(a, b) ((a) > (b) ? (a) : (b))
#define min(a, b) ((a) < (b) ? (a) : (b))
#define out(x, k) cout << fixed << setprecision(k) << x << ed

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;
typedef double db;


const int INF = 1e9;
const int N = 1e5 + 10;
int n, m;
int a[N], b[N];
string now ;
map<string, PII> dir;

bool check_n(int x)
{
	return (x >= 1 && x <= n);
}
 
bool check_m(int y)
{
	return (y >= 1 && y <= m);
}

void solve() {
    
    int i1, j1, i2, j2;
	cin >> n >> m >> i1 >> j1 >> i2 >> j2 >> now; 
	map<int, map<string, int>> vis;
	dir["DL"] = {1, -1}, dir["DR"] = {1, 1}, dir["UR"] = {-1, 1}, dir["UL"] = {-1, -1};
	// 先定义四个方向对应的操作
	//然后我们撞墙的时候方向是相反变化的，比如上下撞墙了 D <-> U , 左右撞墙了 L <-> R 
	if(i1 == i2 && j1 == j2) {    // 先特判掉不需要走就结束的 
		cout << 0 << endl;
		return ;
	}
	int cnt = 0;
	while(1) {
		if(vis[(i1 - 1) * m + j1][now]) {     // 走进循环了 
			cout << "-1" << endl;
			return ;
		}
		vis[(i1 - 1) * m + j1][now] = 1;      // 记录一下，当前状态已经被走了 
		i1 += dir[now].x, j1 += dir[now].y;
		if(!check_n(i1) || !check_m(j1)) {    // 撞墙了 
			cnt ++ ;     
			int tmp1 = i1 - dir[now].x, tmp2 = j1 - dir[now].y;   // 记录一下撞墙之前的位置 
			if(!check_n(i1)) {     // 上下撞墙了 
				if(now[0] == 'D') now[0] = 'U';
				else now[0] = 'D';
			}
			if(!check_m(j1)){      // 左右撞墙了 
				if(now[1] == 'L') now[1] = 'R';
				else now[1] = 'L';
			}
			i1 = tmp1 + dir[now].x, j1 = tmp2 + dir[now].y;       // 把方向改正确之后，求出现在的位置 
		}
		if(i1 == i2 && j1 == j2) break;
	}
	cout << cnt << ed;
	return;

}
int main()
{
    IOS;
    int _ = 1;
    cin >> _;
    
    while(_--) {
        solve();
    }
    
    re;
}