算法练习专栏——Codeforces——Codeforces Round 947 (Div. 1 + Div. 2)

A. Bazoka and Mocha’s Array

Mocha likes arrays, so before her departure, Bazoka gave her an array $a$ consisting of $n$ positive integers as a gift.

Now Mocha wants to know whether array $a$ could become sorted in non-decreasing order after performing the following operation some (possibly, zero) times:

Split the array into two parts — a prefix and a suffix, then swap these two parts. In other words, let $a=x+y$. Then, we can set $a:= y+x$. Here $+$ denotes the array concatenation operation.

For example, if $a=[3,1,4,1,5]$, we can choose $x=[3,1]$ and $y=[4,1,5]$, satisfying $a=x+y$. Then, we can set $a:= y + x = [4,1,5,3,1]$. We can also choose $x=[3,1,4,1,5]$ and $y=[,]$, satisfying $a=x+y$. Then, we can set $a := y+x = [3,1,4,1,5]$. Note that we are not allowed to choose $x=[3,1,1]$ and $y=[4,5]$, neither are we allowed to choose $x=[1,3]$ and $y=[5,1,4]$, as both these choices do not satisfy $a=x+y$.

Input

Each test contains multiple test cases. The first line contains the number of test cases $t$ ($1\leq t\leq 1000$). The description of the test cases follows.

The first line of each test case contains a single integer $n$ ($2\leq n\leq 50$) — the length of the array $a$.

The second line of each test case contains $n$ integers $a_1,a_2,\ldots,a_n$ ($1\leq a_i \leq 10^6$) — the elements of array $a$.

Output

For each test case, output “Yes” if $a$ could become non-decreasing after performing the operation any number of times, and output “No” if not.

You can output “Yes” and “No” in any case (for example, strings “yEs”, “yes”, “Yes” and “YES” will be recognized as a positive response).

Example

input

3
6
1 1 4 5 1 4
5
7 9 2 2 3
3
1 2 3

output

1
2
3

No
Yes
Yes

翻译

378QAQ 是一棵有 $n$ 个顶点的树。初始时，所有顶点都是白色的。

树上有两颗棋子，分别叫做 $P_A$ 和 $P_B$ 。 $P_A$ 和 $P_B$ 最初分别位于顶点 $a$ 和 $b$ 。在一个步骤中，378QAQ 将依次执行以下操作：

将 $P_A$ 移动到邻近顶点。如果目标顶点为白色，则将此顶点涂为红色。
将 $P_B$ 移至相邻顶点。如果目标顶点为红色，则此顶点将被涂抹为蓝色。

最初，顶点 $a$ 会被涂成红色。如果是 $a=b$ ，顶点 $a$ 将被涂成蓝色。请注意，每一步都必须***移动两个棋子。任何时候都可以有两个棋子位于同一个顶点上。

378QAQ 想知道将所有顶点都涂成蓝色所需的最少步数。

输入

每个测试包含多个测试用例。第一行包含测试用例的数量 $t$ （ $1\leq t\leq 10^4$ ）。( $1\leq t\leq 10^4$ ).测试用例说明如下。

每个测试用例的第一行包含一个整数 $n$ ( $1\leq n\leq 2\cdot 10^5$ )。

每个测试用例的第二行包含两个整数 $a$ 和 $b$ ( $1\leq a,b\leq n$ )。

然后是 $n - 1$ 行，每行包含两个整数 $x_i$ 和 $y_i$ （ $1 \le x_i,y_i \le n$ ），表示顶点 $x_i$ 和 $y_i$ 之间有一条边。可以保证这些边构成一棵树。

保证所有测试用例中 $n$ 的总和不超过 $2\cdot 10^5$ 。

输出

对于每个测试用例，输出将所有顶点涂成蓝色所需的最少步骤数。

Example

input

3
6
1 1 4 5 1 4
5
7 9 2 2 3
3
1 2 3

output

1
2
3

No
Yes
Yes

代码

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;
const int N = 60;
int a[N];

void solve() {
    int n, k;
    int max1 = 0, max2 = 0;
    bool flag = true;
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i];
    int count = 0;
    for (int i = 1; i <= n; i++) {
        count += a[i] <= a[i % n + 1];
    }
    if (count < n - 1) cout << "NO\n";
    else cout << "YES\n";
}
int main()
{
    ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
    int _;
    cin >> _;
    while (_--) {
        solve();
    }
}

B. 378QAQ and Mocha’s Array

原题

Mocha likes arrays, so before her departure, 378QAQ gave her an array $a$ consisting of $n$ positive integers as a gift.

Mocha thinks that $a$ is beautiful if there exist two numbers $i$ and $j$ ($1\leq i,j\leq n$, $i\neq j$) such that for all $k$ ($1 \leq k \leq n$), $a_k$ is divisible$^\dagger$ by either $a_i$ or $a_j$.

Determine whether $a$ is beautiful.

$^\dagger$ $x$ is divisible by $y$ if there exists an integer $z$ such that $x = y \cdot z$.

Input

Each test contains multiple test cases. The first line contains the number of test cases $t$ ($1\leq t\leq 500$). The description of the test cases follows.

The first line of each test case contains a single integer $n$ ($3\leq n\leq 10^5$) — the length of the array $a$.

The second line of each test case contains $n$ integers $a_1,a_2,\ldots,a_n$ ($1\leq a_i \leq 10^9$) — the elements of the array $a$.

It is guaranteed that the sum of $n$ over all test cases does not exceed $10^5$.

Output

For each test case, output “Yes” if array $a$ is beautiful, and output “No” otherwise.

You can output “Yes” and “No” in any case (for example, strings “yEs”, “yes”, “Yes” and “YES” will be recognized as a positive response).

Example

input

4
3
7 3 8
5
7 1 9 3 5
5
4 12 2 6 3
5
7 49 9 3 1000000000

output

No
Yes
Yes
No

思路

代码

#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>

using namespace std;
const int N = 1e6 + 10;
int n;
int a[N];

void solve() {
    int n;
	cin >> n;
	for (int i = 1; i <= n; i++) {
		cin >> a[i];
	}
	sort(a + 1, a + n + 1);
	vector<int> b;

	for (int i = 1; i <= n; i++) {
		if(a[i] % a[1] != 0) {
			b.push_back(a[i]);
		}
	}
    if (size(b) == 0) {
        cout << "YES\n";
        return;
    }

    int win = 1;
    if (size(b) == 1) {
        cout << "YES\n";
        return;
    }

	for (int i = 1; i <= size(b) - 1; i++) {
		win &= (b[i] % b[0] == 0);
	}
	if(win) cout << "YES\n";
	else cout << "NO\n";
}

int main()
{
    int t;
    cin >> t;
    while (t--) {
        solve();
    }

    return 0;
}

C. Chamo and Mocha’s Array

原题

Mocha likes arrays, so before her departure, Chamo gave her an array $a$ consisting of $n$ positive integers as a gift.

Mocha doesn’t like arrays containing different numbers, so Mocha decides to use magic to change the array. Mocha can perform the following three-step operation some (possibly, zero) times:

Choose indices $l$ and $r$ ($1 \leq l < r \leq n$)
Let $x$ be the median$^\dagger$ of the subarray $[a_l, a_{l+1},\ldots, a_r]$
Set all values $a_l, a_{l+1},\ldots, a_r$ to $x$

Suppose $a=[1,2,3,4,5]$ initially:

If Mocha chooses $(l,r)=(3,4)$ in the first operation, then $x=3$, the array will be changed into $a=[1,2,3,3,5]$.
If Mocha chooses $(l,r)=(1,3)$ in the first operation, then $x=2$, the array will be changed into $a=[2,2,2,4,5]$.

Mocha will perform the operation until the array contains only the same number. Mocha wants to know what is the maximum possible value of this number.

$^\dagger$ The median in an array $b$ of length $m$ is an element that occupies position number $\lfloor \frac{m+1}{2} \rfloor$ after we sort the elements in non-decreasing order. For example, the median of $[3,1,4,1,5]$ is $3$ and the median of $[5,25,20,24]$ is $20$.

Input

Each test contains multiple test cases. The first line contains the number of test cases $t$ ($1\leq t\leq 500$). The description of the test cases follows.

The first line of each test case contains a single integer $n$ ($2\leq n\leq 10^5$) — the length of the array $a$.

The second line of each test case contains $n$ integers $a_1,a_2,\ldots,a_n$ ($1\leq a_i \leq 10^9$) — the elements of the array $a$.

It is guaranteed that the sum of $n$ over all test cases does not exceed $10^5$.

Output

For each test case, output the maximum value of the number.

Example

input

output

1
2

1
4

Note

In the first test case, $a=[1,2]$. Mocha can only choose the interval $(l,r)=(1,2)$. The array will be changed to $a=[1,1]$. Therefore, the answer is $1$.

In the second test case, Mocha can perform the following operations:

Choose the interval $(l,r)=(4,5)$, then $a=[1,2,3,4,4]$.
Choose the interval $(l,r)=(3,5)$, then $a=[1,2,4,4,4]$.
Choose the interval $(l,r)=(1,5)$, then $a=[4,4,4,4,4]$.

The array contains only the same number, which is $4$. It can be proven that the maximum value of the final number cannot be greater than $4$.

思路

代码

D. Paint the Tree

原题

378QAQ has a tree with $n$ vertices. Initially, all vertices are white.

There are two chess pieces called $P_A$ and $P_B$ on the tree. $P_A$ and $P_B$ are initially located on vertices $a$ and $b$ respectively. In one step, 378QAQ will do the following in order:

Move $P_A$ to a neighboring vertex. If the target vertex is white, this vertex will be painted red.
Move $P_B$ to a neighboring vertex. If the target vertex is colored in red, this vertex will be painted blue.

Initially, the vertex $a$ is painted red. If $a=b$, the vertex $a$ is painted blue instead. Note that both the chess pieces must be moved in each step. Two pieces can be on the same vertex at any given time.

378QAQ wants to know the minimum number of steps to paint all vertices blue.

Input

Each test contains multiple test cases. The first line contains the number of test cases $t$ ($1\leq t\leq 10^4$). The description of the test cases follows.

The first line of each test case contains one integer $n$ ($1\leq n\leq 2\cdot 10^5$).

The second line of each test case contains two integers $a$ and $b$ ($1\leq a,b\leq n$).

Then $n - 1$ lines follow, each line contains two integers $x_i$ and $y_i$ ($1 \le x_i,y_i \le n$), indicating an edge between vertices $x_i$ and $y_i$. It is guaranteed that these edges form a tree.

It is guaranteed that the sum of $n$ over all test cases does not exceed $2\cdot 10^5$.

Output

For each test case, output the minimum number of steps to paint all vertices blue.

Example

input

output

1
2
3

2
8
13

Note

In the first test case, 378QAQ can paint all vertices blue in the following order:

Initially, $P_A$ is located on the vertex $1$, and $P_B$ is located on the vertex $2$. The vertex $1$ is painted red and the vertex $2$ is white.
378QAQ moves $P_A$ to the vertex $2$ and paints it red. Then 378QAQ moves $P_B$ to the vertex $1$ and paints it blue.
378QAQ moves $P_A$ to the vertex $1$. Then 378QAQ moves $P_B$ to the vertex $2$ and paints it blue.

思路

代码

E. Chain Queries

原题

You are given a tree of $n$ vertices numbered from $1$ to $n$. Initially, all vertices are colored white or black.

You are asked to perform $q$ queries:

“u” — toggle the color of vertex $u$ (if it was white, change it to black and vice versa).

After each query, you should answer whether all the black vertices form a chain. That is, there exist two black vertices such that the simple path between them passes through all the black vertices and only the black vertices. Specifically, if there is only one black vertex, they form a chain. If there are no black vertices, they do not form a chain.

Input

Each test contains multiple test cases. The first line contains the number of test cases $t$ ($1\leq t\leq 10^4$). The description of the test cases follows.

The first line of each test case contains two integers $n$ and $q$ ($1\leq n,q\leq 2\cdot 10^5$).

The second line of each test case contains $n$ integers $c_1,c_2,\ldots,c_n$ ($c_i \in { \mathtt{0}, \mathtt{1} }$) — the initial color of the vertices. $c_i$ denotes the color of vertex $i$ where $\mathtt{0}$ denotes the color white, and $\mathtt{1}$ denotes the color black.

Then $n - 1$ lines follow, each line contains two integers $x_i$ and $y_i$ ($1 \le x_i,y_i \le n$), indicating an edge between vertices $x_i$ and $y_i$. It is guaranteed that these edges form a tree.

The following $q$ lines each contain an integer $u_i$ ($1 \le u_i \le n$), indicating the color of vertex $u_i$ needs to be toggled.

It is guaranteed that the sum of $n$ and $q$ over all test cases respectively does not exceed $2\cdot 10^5$.

Output

For each query, output “Yes” if the black vertices form a chain, and output “No” otherwise.

You can output “Yes” and “No” in any case (for example, strings “yEs”, “yes”, “Yes” and “YES” will be recognized as a positive response).

Examples

input

output

No
No
Yes
Yes
No

input

output

Yes
No
Yes
Yes
Yes
Yes
No
No
Yes

Note

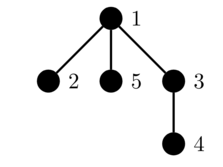
In the second test case, the color of the vertices are as follows:

The initial tree:

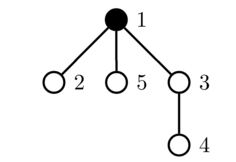
The first query toggles the color of vertex $4$:

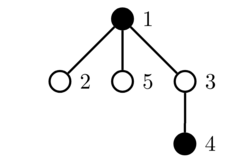
The second query toggles the color of vertex $3$:

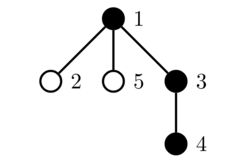
The third query toggles the color of vertex $2$:

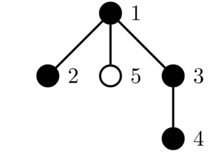
The fourth query toggles the color of vertex $5$:

翻译

给你一棵由 $n$ 个顶点组成的树，这些顶点的编号从 $1$ 到 $n$ 不等。最初，所有顶点都被染成白色或黑色。

您需要执行 $q$ 次查询：

u” - 切换顶点 $u$ 的颜色（如果是白色，则将其变为黑色，反之亦然）。

每次查询后，您都应该回答所有黑色顶点是否形成一条链。也就是说，是否存在两个黑色顶点，使得它们之间的简单路径通过所有黑色顶点且只通过黑色顶点。具体来说，如果只有一个黑色顶点，它们就会形成一条链。如果没有黑色顶点，则它们***不构成链。

输入

每个测试包含多个测试用例。第一行包含测试用例的数量 $t$ ( $1\leq t\leq 10^4$ )。测试用例说明如下。

每个测试用例的第一行包含两个整数 $n$ 和 $q$ ( $1\leq n,q\leq 2\cdot 10^5$ )。

每个测试用例的第二行包含 $n$ 个整数 $c_1,c_2,\ldots,c_n$ ( $c_i \in { \mathtt{0}, \mathtt{1} }$ ) - 顶点的初始颜色。 $c_i$ 表示顶点 $i$ 的颜色，其中 $\mathtt{0}$ 表示白色， $\mathtt{1}$ 表示黑色。

接着是 $n - 1$ 行，每行包含两个整数 $x_i$ 和 $y_i$ （ $1 \le x_i,y_i \le n$ ），表示顶点 $x_i$ 和 $y_i$ 之间的一条边。可以保证这些边构成一棵树。

下面的 $q$ 行分别包含一个整数 $u_i$ ( $1 \le u_i \le n$ )，表示需要切换顶点 $u_i$ 的颜色。

保证所有测试案例中 $n$ 和 $q$ 的总和不超过 $2\cdot 10^5$ 。

输出

对于每个查询，如果黑色顶点形成链，则输出 “是”，否则输出 “否”。

您可以在任何情况下输出 “Yes “和 “No”（例如，字符串 “yEs”、”yes”、”Yes “和 “YES “将被识别为肯定回答）。

Examples

input

output

No
No
Yes
Yes
No

input

output

Yes
No
Yes
Yes
Yes
Yes
No
No
Yes

注

在第二个测试案例中，顶点的颜色如下：

初始树

第一个查询会切换顶点 $4$ 的颜色：

第二个查询会切换顶点 $3$ 的颜色：

第三个查询会切换顶点 $2$ 的颜色：

第四个查询会切换顶点 $5$ 的颜色：

思路

代码

爬虫学习基础——爬虫学习基础篇上一篇

算法练习专栏——牛客练习——牛客周赛 Round 44 下一篇